
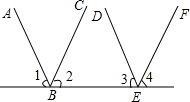
 完成下列推理说明:
完成下列推理说明: 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源:2016-2017学年江苏省无锡市八年级3月份阶段性检测数学试卷(解析版) 题型:解答题
如图,在△ABC中,AB=AC,D为BC中点,四边形ABDE是平行四边形,求证:四边形ADCE是矩形。

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角∠O的内部有一滑动杆AB=10cm,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动.
如图,在直角∠O的内部有一滑动杆AB=10cm,当端点A沿直线AO向下滑动时,端点B会随之自动地沿直线OB向左滑动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com