
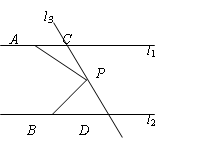
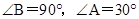 ;图②中,
;图②中,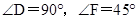 .图③是该同学所做的一个实验:他将△
.图③是该同学所做的一个实验:他将△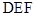 的直角边
的直角边 与△
与△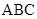 的斜边
的斜边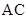 重合在一起,并将△
重合在一起,并将△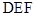 沿
沿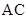 方向移动.在移动过程中,
方向移动.在移动过程中,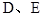 两点始终在
两点始终在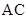 边上(移动开始时点
边上(移动开始时点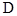 与点
与点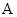 重合).
重合).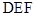 沿
沿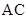 方向移动的过程中,该同学发现:
方向移动的过程中,该同学发现: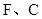 两点间的距离 ;连接
两点间的距离 ;连接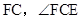 的度数 .(填“不变”、“ 逐渐变大”或“逐渐变小”)
的度数 .(填“不变”、“ 逐渐变大”或“逐渐变小”)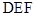 在移动过程中,
在移动过程中,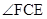 与
与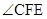 度数之和是否为定值,请加以说明;
度数之和是否为定值,请加以说明;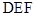 移动至某位置,使
移动至某位置,使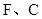 的连线与
的连线与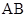 平行?如果能,请求出此时
平行?如果能,请求出此时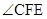 的度数,如果不能,请说明理由。
的度数,如果不能,请说明理由。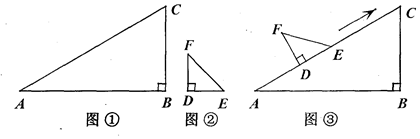


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 a°, 则下列结论:
a°, 则下列结论: 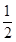 (180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.
(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.| A.1 | B.2 | C.3 | D.4 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
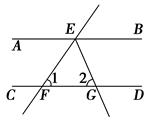
| A.50° | B.60° | C.65° | D.90° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com