
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпЕФЖЅЕузјБъЮЊMЃЈ1ЃЌ4ЃЉЃЌЧвОЙ§ЕуNЃЈ2ЃЌ3ЃЉЃЌгыxжсНЛгкAЁЂBСНЕуЃЈЕуAдкЕуBзѓВрЃЉЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєжБЯпy=kx+tОЙ§CЁЂMСНЕуЃЌЧвгыxжсНЛгкЕуDЃЌЪджЄУїЫФБпаЮCDANЪЧЦНааЫФБпаЮЃЛ
ЃЈ3ЃЉЕуPдкХзЮяЯпЕФЖдГЦжсx=1ЩЯдЫЖЏЃЌЧыЬНЫїЃКдкxжсЩЯЗНЪЧЗёДцдкетбљЕФPЕуЃЌЪЙвдPЮЊдВаФЕФдВОЙ§AЁЂBСНЕуЃЌВЂЧвгыжБЯпCDЯрЧаЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
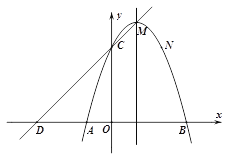
ЁОД№АИЁП(1)y =-x2+2x+3;(2)жЄУїМћНтЮіЃЛЃЈ3ЃЉТњзуЬтвтЕФЕуPДцдкЃЌЦфзјБъЮЊЃЈ1ЃЌ ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁПЃЈ1ЃЉНтЃКгЩХзЮяЯпЕФЖЅЕуЪЧMЃЈ1ЃЌ4ЃЉЃЌ
ЩшНтЮіЪНЮЊy=aЃЈx-1ЃЉ2+4ЃЈaЃМ0ЃЉ
гжХзЮяЯпОЙ§ЕуNЃЈ2ЃЌ3ЃЉЃЌ
Ыљвд3=aЃЈ2-1ЃЉ2+4ЃЌНтЕУa=-1
ЫљвдЫљЧѓХзЮяЯпЕФНтЮіЪНЮЊy=-ЃЈx-1ЃЉ2+4=-x2+2x+3
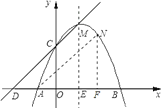
ЃЈ2ЃЉжЄУїЃКжБЯпy=kx+tОЙ§C(0,3)ЁЂMЃЈ1ЃЌ4ЃЉСНЕуЃЌ
 Ёр
Ёр![]() ,МДk=1ЃЌt=3ЃЌМДЃКжБЯпНтЮіЪНЮЊy=x+3Ё4Зж
,МДk=1ЃЌt=3ЃЌМДЃКжБЯпНтЮіЪНЮЊy=x+3Ё4Зж
ЧѓЕУA(-1ЃЌ0),D(-3ЃЌ0)ЃЌЁрAD=2
ЁпC(0,3), NЃЈ2ЃЌ3ЃЉ
ЁрCN=2= ADЃЌЧвCNЁЮAD
ЁрЫФБпаЮCDANЪЧЦНааЫФБпаЮЃЎЁЁЁЁЁ6Зж
ЃЈ3ЃЉНтЃКМйЩшдкxжсЩЯЗНДцдкетбљЕФPЕуЃЌЪЙвдPЮЊдВаФЕФдВОЙ§AЁЂBСНЕуЃЌВЂЧвгыжБЯпCDЯрЧаЃЌЩшPЃЈ1ЃЌuЃЉЦфжаuЃО0ЃЌ
дђPAЪЧдВЕФАыОЖЧвPA2=u2+22Й§PзіжБЯпCDЕФДЙЯпЃЌДЙзуЮЊQЃЌдђPQ=PAЪБвдPЮЊдВаФЕФдВгыжБЯпCDЯрЧаЃЎ
гЩЕкЃЈ2ЃЉаЁЬтвзЕУЃКЁїMDEЮЊЕШбќжБНЧШ§НЧаЮЃЌЙЪЁїPQMвВЪЧЕШбќжБНЧШ§НЧаЮЃЌ
гЩPЃЈ1ЃЌuЃЉЕУPE=uЃЌPM=|4-u|ЃЌPQ=![]()
гЩPQ2=PA2ЕУЗНГЬЃК![]() =u2+22ЃЌ ЁЁЁЁЁЁЁЁЁЁЁЁЁЁ8Зж
=u2+22ЃЌ ЁЁЁЁЁЁЁЁЁЁЁЁЁЁ8Зж
НтЕУ![]() ЃЌЩсШЅИКжЕu=
ЃЌЩсШЅИКжЕu=![]() ЃЌЗћКЯЬтвтЕФu=
ЃЌЗћКЯЬтвтЕФu=![]() ЃЌЁЁЁЁ9Зж
ЃЌЁЁЁЁ9Зж
ЫљвдЃЌТњзуЬтвтЕФЕуPДцдкЃЌЦфзјБъЮЊЃЈ1ЃЌ![]() ЃЉЃЎЁ
ЃЉЃЎЁ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЕу![]() дке§БШР§КЏЪ§ЭМЯѓЩЯЃЌЕу
дке§БШР§КЏЪ§ЭМЯѓЩЯЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯвдУПУы2ИіЕЅЮЛЕФЫйЖШгЩЕу
ЩЯвдУПУы2ИіЕЅЮЛЕФЫйЖШгЩЕу![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌЕу
дЫЖЏЃЌЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯгЩЕу
ЩЯгЩЕу![]() ЯђЕу
ЯђЕу![]() дЫЖЏЃЌ
дЫЖЏЃЌ![]() СНЕуЭЌЪБдЫЖЏЃЌЭЌЪБЭЃжЙЃЌдЫЖЏЪБМфЮЊ
СНЕуЭЌЪБдЫЖЏЃЌЭЌЪБЭЃжЙЃЌдЫЖЏЪБМфЮЊ![]() УыЃЎ
УыЃЎ
ЃЈ1ЃЉе§БШР§КЏЪ§ЕФЙиЯЕЪНЮЊ ЃЛ
ЃЈ2ЃЉЕБ![]() УыЃЌЧв
УыЃЌЧв![]() ЪБЃЌЧѓЕу
ЪБЃЌЧѓЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉСЌНг![]() ЃЌдкЕу
ЃЌдкЕу![]() дЫЖЏЙ§ГЬжаЃЌ
дЫЖЏЙ§ГЬжаЃЌ![]() гы
гы![]() ЪЧЗёШЋЕШЃПШчЙћШЋЕШЃЌЧыЧѓГіЕу
ЪЧЗёШЋЕШЃПШчЙћШЋЕШЃЌЧыЧѓГіЕу![]() ЕФдЫЖЏЫйЖШЃЛШчЙћВЛШЋЕШЃЌЧыЫЕУїРэгЩЃЎ
ЕФдЫЖЏЫйЖШЃЛШчЙћВЛШЋЕШЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЕуOЕНЁїABCЕФСНБпABЃЌACЫљдкжБЯпЕФОрРыЯрЕШЃЌЧвOB=OCЃЎ
(1)ШчЭМ1ЃЌШєЕуOдкБпBCЩЯЃЌOEЁЭABЃЌOFЁЭACЃЌДЙзуЗжБ№ЮЊEЃЌFЃЎЧѓжЄЃКAB=ACЃЛ

(2)ШчЭМЃЌШєЕуOдкЁїABCЕФФкВПЃЌЧѓжЄЃКAB=ACЃЛ
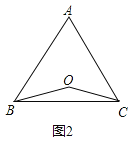
(3)ШєЕуOдкЁїABCЕФЭтВПЃЌAB=ACГЩСЂТ№ЃПЧыЛГіЭМБэЪОЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГСОЦћГЕгЭЯфжадгаЦћгЭ60![]() ЃЌЦћГЕУПааЪЛ50
ЃЌЦћГЕУПааЪЛ50![]() КФгЭ6
КФгЭ6![]()
ЃЈ1ЃЉЭъГЩЯТБэ
ЦћГЕааЪЛТЗГЬ | 0 | 50 | 100 | 150 |
КФгЭСП | __________ | __________ | __________ | __________ |
ЃЈ2ЃЉаДГіКФгЭСП![]() гыЦћГЕааЪЛТЗГЬ
гыЦћГЕааЪЛТЗГЬ![]() жЎМфЕФЙиЯЕЪН
жЎМфЕФЙиЯЕЪН
ЃЈ3ЃЉЧѓГігЭЯфЪЃгргЭСП![]() гыЦћГЕааЪЛТЗГЬ
гыЦћГЕааЪЛТЗГЬ![]() жЎМфЕФЙиЯЕЪНТ№ЃП
жЎМфЕФЙиЯЕЪНТ№ЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
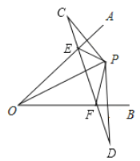
ЁОЬтФПЁПдкЁбOжаЃЌABЮЊжБОЖЃЌCЮЊЁбOЩЯвЛЕуЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЙ§ЕуCзїЁбOЕФЧаЯпЃЌгыABЕФбгГЄЯпЯрНЛгкЕуPЃЌШєЁЯCAB=28ЁуЃЌЧѓЁЯPЕФДѓаЁЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌDЮЊЛЁABЩЯвЛЕуЃЌЧвODОЙ§ACЕФжаЕуEЃЌСЌНгDCВЂбгГЄЃЌгыABЕФбгГЄЯпЯрНЛгкЕуPЃЌШєЁЯCAB=10ЁуЃЌЧѓЁЯPЕФДѓаЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABC жаЃЌADЁЭBC гкЕу DЃЌЕу E ЮЊBDБпЩЯвЛЕуЃЌЙ§Еу E зї EGЁЮADЃЌЗжБ№НЛ AB КЭ CA ЕФбгГЄЯпгкЕу FЃЌGЃЌЁЯAFG=ЁЯGЃЎ

ЃЈ1ЃЉжЄУїЃКЁїABDЁеЁїACD
ЃЈ2ЃЉШєЁЯB=40ЁуЃЌжБНгаДГіЁЯFAG= Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЪЧ
ЪЧ![]() ФкШЮвтвЛЕуЃЌ
ФкШЮвтвЛЕуЃЌ![]() ЃЌЕу
ЃЌЕу![]() гыЕу
гыЕу![]() ЙигкЩфЯп
ЙигкЩфЯп![]() ЖдГЦЃЌЕу
ЖдГЦЃЌЕу![]() гыЕу
гыЕу![]() ЙигкЩфЯп
ЙигкЩфЯп![]() ЖдГЦЃЌСЌНг
ЖдГЦЃЌСЌНг![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌЕБ
ЃЌЕБ![]() ЕФжмГЄЪЧ5
ЕФжмГЄЪЧ5![]() ЪБЃЌ
ЪБЃЌ![]() ЕФЖШЪ§ЪЧ______ЖШЃЎ
ЕФЖШЪ§ЪЧ______ЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
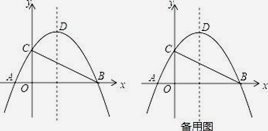
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2Љ3axЉ4aЕФЭМЯѓОЙ§ЕуCЃЈ0ЃЌ2ЃЉЃЌНЛxжсгкЕуAЁЂBЃЈAЕудкBЕузѓВрЃЉЃЌЖЅЕуЮЊDЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНМАЕуAЁЂBЕФзјБъЃЛ
ЃЈ2ЃЉНЋЁїABCбижБЯпBCЖделЃЌЕуAЕФЖдГЦЕуЮЊAЁфЃЌЪдЧѓAЁфЕФзјБъЃЛ
ЃЈ3ЃЉХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдкЕуPЃЌЪЙЁЯBPC=ЁЯBACЃПШєДцдкЃЌЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаСНЖЮВФСЯЃЌЛиД№ЮЪЬтЃК
ВФСЯвЛ:AЃЈx1ЃЎy1)ЃЌB(x2ЃЎy2)ЕФжаЕузјБъЮЊ(![]() ЃЌ
ЃЌ![]() ) Р§ШчЃЌЕу(1ЃЌ5)ЃЌ(3ЃЌ-1)ЕФжаЕузјБъЮЊ(
) Р§ШчЃЌЕу(1ЃЌ5)ЃЌ(3ЃЌ-1)ЕФжаЕузјБъЮЊ(![]() ЃЌ
ЃЌ![]() )ЃЌМД(2ЃЌ 2)
)ЃЌМД(2ЃЌ 2)
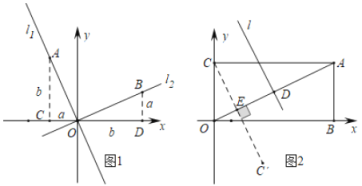
ВФСЯЖўЃКШчЭМ1ЃЌе§БШР§КЏЪ§l1:y=k1xКЭl2:y=k2xЕФЭМЯёЯрЛЅДЙжБЃЌЗжБ№дкl1КЭl2ЩЯШЁЕуAЁЂBЃЌЪЙЕУAO=BOЃЎЗжБ№Й§ЕуAЁЂBзїxжсЕФДЙЯпЃЌДЙзуЗжБ№ЮЊЕуCЁЂDЃЎЯдШЛЁїAOCЁеЁї OBDЃЎЩшOC=BD=aЃЌAC=OD=bЃЎдђAЃЈ-aЃЌbЃЉЃЌB(bЃЌa)ЃЎгкЪЧ![]() ЃЌЫљвдk1k2ЕФжЕЮЊвЛИіГЃЪ§ЃЎ
ЃЌЫљвдk1k2ЕФжЕЮЊвЛИіГЃЪ§ЃЎ
ЃЈ1ЃЉдкВФСЯЖўжаЃЌk1k2=____ (аДГіетИіГЃЪ§ОпЬхЕФжЕ) ЃЛ
ЃЈ2ЃЉШчЭМЃЌдкОиаЮOBACжаAЃЈ4ЃЌ2ЃЉЃЌЕуDЪЧOAжаЕуЃЌгУСНЖЮВФСЯЕФНсТлЃЌЧѓЕуDЕФзјБъКЭOAЕФДЙжБЦНЗжЯпlЕФНтЮіЪНЃЛ
ЃЈ3ЃЉШєЕуCЁЏ гыЕуCЙигкOAЖдГЦЃЌгУСНЖЮВФСЯЕФНсТлЃЌЧѓЕуC'ЕФзјБъЃЌ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com