练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

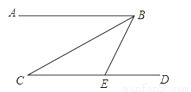
    如图，已知AB∥CD，BC平分∠ABE，∠C=34°，则∠BED=________．

    68° 【解析】如图， ∵BC平分∠ABE，∴∠1=∠2， 又∵AB∥CD，∴∠C=∠1， ∴∠1=∠2=∠C=34°， 又∠BED是△BCE的外角， ∴∠BED=∠2+∠C=68°. 故答案为68°.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：陕西省2018届九年级上学期期中考试数学试卷 题型：解答题

    （本题满分分）小明、小华在一栋高楼前感慨楼房真高．小明说：“这楼起码层！”小华却不以为然：“层？我看没有！”小明说：“有本事，就让我们一起来测量吧！”

    如图，矩形表示楼体，小明、小华在楼体两侧各选、两点，使得、、、四点在同一直线上，利用皮尺和侧倾器测得如下数据， 米， 米， ， ．

    （）请你帮助他们算一算楼高．（结果保留根号）

    （）若每层楼按米计算，你支持小明还是小华的观点呢？请说明理由．

    （）楼高米．（）CF=51.24米<3×20米，支持小华． 【解析】试题分析：（1）设楼高为，则，在和中分别用表示的值，然后根据求出的值即可； （2）根据（1）求出的楼高，然后求出20层楼的高度，比较和20层楼高的大小即可判断谁的观点正确． 试题解析: (1)设楼高为x米，则CF=DE=x米， 米，BD=x米， 解得 (米)， ∴楼高米. (2) 米<3×20...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省哈尔滨市双城区七年级（上）期末数学试卷（五四学制） 题型：解答题

    某车间有技术工85人，平均每天每人可加工甲种部件16个或乙种部件10个，2个甲种部件和3个乙种部件配 一套，问加工甲、乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套？（4分）

    甲：25人 乙60人 【解析】 试题分析：首先设安排甲部件x个人，则（85－x）人生产乙部件，根据甲零件数量的3倍等于乙零件数量 的2倍列出方程进行求解. 试题解析：设甲部件安排x人,乙部件安排（85-x）人才能使每天加工的甲、乙两种部件刚好配套 由题意得：3×16x=2×10（85－x） 解得：x=25 则85－x=85－25=60（人） 答：甲部件安排20人...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年黑龙江省哈尔滨市双城区七年级（上）期末数学试卷（五四学制） 题型：单选题

    如图，把一个正方形对折两次后沿虚线剪下，展开后所得到的图形是( )

    A. B. C. D.

    B 【解析】试题分析：此类问题只有动手操作一下，按照题意的顺序折叠，剪开，观察所得的图形，可得正确的选项B． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册数学第五章相交线与平行线单元检测卷 题型：解答题

    如图，EF∥AD，∠1=∠2，∠BAC=70°，

    （1）DG平行AB吗？请说明理由.

    （2）求∠AGD的度数．

    （1）见解析；（2）110° 【解析】试题分析： （1）只需判断出∠1与∠3这一对内错角是否相等即可； （2）∠AGD与∠ABC为同旁内角，由（1）知DG//AB,l利用平行线性质即可求出∠AGD. 【解析】 （1）DG平行AB. 理由：∵EF∥AD， ∴∠2=∠3， ∵∠1=∠2， ∴∠1=∠3， ∴DG∥AB， （2）【解析】 ∵DG∥...

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册数学第五章相交线与平行线单元检测卷 题型：填空题

    如图：△ABC中，∠A的同旁内角是________ ．

    ∠B和∠C 【解析】当AB为截线时，∠A与∠B为同旁内角；当AC为截线时，∠A与∠C为同旁内角. 故答案为∠B和∠C.

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级下册数学第五章相交线与平行线单元检测卷 题型：单选题

    将一个直角三角板和一把直尺如图放置，如果∠α=43°，则∠β的度数是（ ）

    A. 43° B. 47° C. 30° D. 60°

    B 【解析】试题解析：如图，延长BC交刻度尺的一边于D点， ∵AB∥DE， ∴∠β=∠EDC， 又∠CED=∠α=43°， ∠ECD=90°， ∴∠β=∠EDC=90°-∠CED=90°-43°=47° 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型：填空题

    在一个不透明的袋子中装有除颜色外其余均相同的7个小球，其中红球2个，黑球5个，若再放入m个一样的黑球并摇匀，此时，随机摸出一个球是黑球的概率等于，则m的值为 ．

    3． 【解析】 试题分析：根据题意得：=，解得：m=3．故答案为：3．

    查看答案和解析>>

    科目：初中数学 来源：湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型：解答题

    （10分）如图①，在△ABC中，∠ACB=2∠B，AD为∠BAC的角平分线，

    求证：AB=AC+CD

    小明同学经过思考，得到如下解题思路：

    在AB上截取AE=AC，连接DE，得到△ADE≌△ADC，从而易证AB=AC+CD

    （1）请你根据以上解思路写出证明过程；

    （2）如图②，若AD为△ABC的外角∠CAE平分线，交BC的延长线于点D，

    ∠D=25°，其他条件不变，求∠B的度数。

    （1）见解析；（2）50° 【解析】试题分析：先根据“SAS”证明△ADE≌△ADC,从而DE=DC, ∠AED=∠ACB,再由外角的性质可得∠B=∠BDE,从而BE=CD，然后利用等量代换证明结论；（2）利用外角的性质和角平分线的定义得到∠CAD= ，然后根据三角形内角和列方程求解. 【解析】 （1）∵AD为∠BAC的角平分线， ∴∠BAD=∠CAD. 在△ADE和△A...

    查看答案和解析>>

    同步练习册答案