
 =7)
=7) =5)
=5)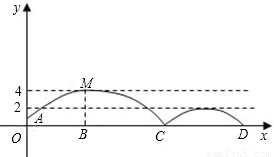
 (x-6)2解得x的值即可知道CD、BD.
(x-6)2解得x的值即可知道CD、BD.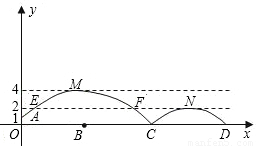 解:(1)(3分)如图,设第一次落地时,
解:(1)(3分)如图,设第一次落地时,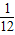 (2分)
(2分) (x-6)2+4,(3分)
(x-6)2+4,(3分) x2+x+1).
x2+x+1). (x-6)2+4=0,
(x-6)2+4=0,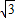 +6≈13,x2=-4
+6≈13,x2=-4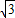 +6<0(舍去).(2分)
+6<0(舍去).(2分) (x-6)2+4解得x1=6-2
(x-6)2+4解得x1=6-2 ,x2=6+2
,x2=6+2 (2分)
(2分) ≈10(3分)
≈10(3分) (x-6)2+4=0
(x-6)2+4=0 (舍),x2=6+4
(舍),x2=6+4 ≈13.∴点C坐标为(13,0).(1分)
≈13.∴点C坐标为(13,0).(1分) (x-k)2+2(2分)
(x-k)2+2(2分)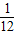 (13-k)2+2=0
(13-k)2+2=0 (舍去),k2=6+4
(舍去),k2=6+4 +2
+2 ≈6+7+5=18(3分)
≈6+7+5=18(3分) (x-18)2+2,x1=18-2
(x-18)2+2,x1=18-2 (舍去),x2=18+2
(舍去),x2=18+2 ≈23,
≈23,

科目:初中数学 来源: 题型:
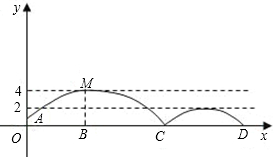 弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.| 3 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 6 |
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(吉林长春卷)数学(带解析) 题型:解答题
如图,足球场上守门员在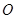 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的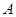 处飞出(
处飞出(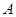 在
在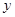 轴上),运动员乙在距
轴上),运动员乙在距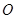 点6米的
点6米的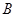 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点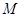 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.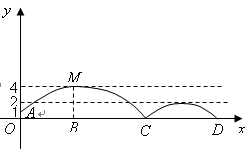
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点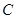 距守门员多少米?(取
距守门员多少米?(取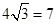 )
)
(3)运动员乙要抢到第二个落点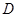 ,他应再向前跑多少米?
,他应再向前跑多少米?
(取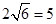 )
)
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江杭州翠苑中学九年级上学期10月质量检测数学试卷(解析版) 题型:解答题
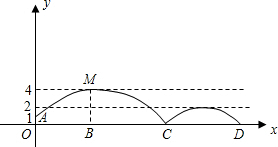
如图,足球场上守门员在O处开出一高球,球从离地面1米的A处飞出(A在y轴上),运动员乙在距O点6米的B处发现球在自己头的正上方达到最高点M,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
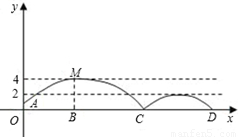
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点C距守门员多少米?(取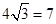 )
)
(3)运动员乙要抢到第二个落点D,他应再向前跑多少米?(取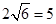 )
)
查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(吉林长春卷)数学(解析版) 题型:解答题
如图,足球场上守门员在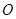 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的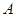 处飞出(
处飞出(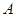 在
在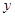 轴上),运动员乙在距
轴上),运动员乙在距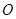 点6米的
点6米的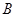 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点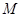 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
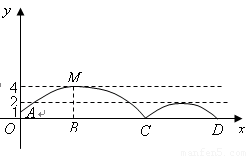
(1)求足球开始飞出到第一次落地时,该抛物线的表达式.
(2)足球第一次落地点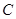 距守门员多少米?(取
距守门员多少米?(取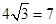 )
)
(3)运动员乙要抢到第二个落点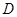 ,他应再向前跑多少米?
,他应再向前跑多少米?
(取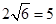 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com