

分析 (1)由于对角线互相垂直,所以四边形ABCD的面积可化为$\frac{1}{2}AO•BD$+$\frac{1}{2}CO•BD$的和;
(2)由于对角线互相垂直,由勾股定理分别表示出AB2、CD2、AD2、BC2;
(3)①过点P作PD⊥AC于点D,构造△PAD∽△BAC后,利用BP2+CQ2=PQ2+BC2列出关于t的方程;
②连接BE、CG、BG、CE,证明四边形BCGE是垂直四边形,然后利用其性质“一组对边的平方和等于另一组对边的平方和”,即可得出EG与BC的数量关系.
解答 解:(1)∵四边形ABCD是“垂直四边形”,
∴AC⊥BD,
∴△ABD的面积为:$\frac{1}{2}AO•BD$,
△CBD的面积为:$\frac{1}{2}CO•BD$,
∴四边形ABCD的面积:$\frac{1}{2}AO•BD$+$\frac{1}{2}CO•BD$
=$\frac{1}{2}$BD(AO+CO)
=$\frac{1}{2}$AC•BD
=$\frac{1}{2}$×8×7
=28;
(2)∵四边形ABCD是“垂直四边形”,
∴AC⊥BD.
由勾股定理可知:
AB2+CD2=(AO2+BO2)+(DO2+CO2),
AD2+BC2=(AO2+DO2)+(BO2+CO2),
∴AB2+CD2=AD2+BC2; (3)①如图2,过点P作PD⊥AC于点D,
(3)①如图2,过点P作PD⊥AC于点D,
由题意知:AP=5t,CQ=6t,
∵∠ACB=90°,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10
∵PD∥BC.
∴△PAD∽△BAC,
∴$\frac{AD}{AC}$=$\frac{PD}{BC}$=$\frac{AP}{AB}$,
∴$\frac{AD}{6}$=$\frac{PD}{8}$=$\frac{5t}{10}$,
∴AD=3t,PD=4t,
∴DQ=AC-AD-CQ=6-9t,
∵四边形BCQP是“垂直四边形”.
∴BP2+CQ2=PQ2+BC2,
∴(10-5t)2+(6t)2=(4t)2+(6-9t)2+82,
∴解得t=$\frac{2}{9}$或t=0(舍去),
∴当四边形BCQP是“垂直四边形”时,t的值为$\frac{2}{9}$;
②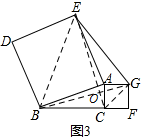 如图3,连接CG、BG、BE、CE,
如图3,连接CG、BG、BE、CE,
CE与BG交于点O
由题意知:EA=BA,AC=AG
∠EAB=∠CAG=90°
∴∠EAB+∠BAC=∠CAG+∠BAC
∴∠EAC=∠BAG
在△EAC与△BAG中
$\left\{\begin{array}{l}{EA=BA}\\{∠EAC=∠BAG}\\{AC=AG}\end{array}\right.$,
∴△EAC≌△BAG(SAS)
∴∠CEA=∠GBA
∴∠EAB=∠BOE=90°
∴四边形BCGE是“垂直四边形”
∴BC2+EG2=BE2+CG2,
∵AB=3AC,
∴EG2=$\frac{3}{2}$BC2.
点评 本题考查新定义型问题,解题的关键是对新定义的理解,涉及到勾股定理,全等三角形的性质与判定,相似三角形的性质与判定等知识内容,题目较新颖和综合,需要学生将新旧知识联系起来.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,有一个直角△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1A1C是由△ABC旋转得到的.
如图,在平面直角坐标系中,有一个直角△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1A1C是由△ABC旋转得到的.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
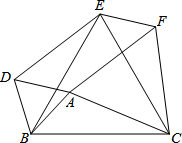 如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.
如图,以△ABC的三边为边,在BC的同侧分别作3个等边三角形,即△ABD、△BCE、△ACF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
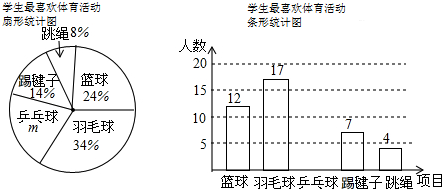
 某学校计划开设A、B、C、D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如下所示的两个不完整统计图表.
某学校计划开设A、B、C、D四门校本课程供学生选修,规定每个学生必须并且只能选修其中一门,为了了解学生的选修意向,现随机抽取了部分学生进行调查,并将调查结果绘制成如下所示的两个不完整统计图表.| 选修课程 | 所占百分比 |
| A | a% |
| B | 25% |
| C | b% |
| D | 20% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com