
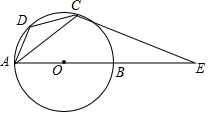
 如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.
如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.分析 (1)欲证明$\widehat{BC}$=$\widehat{DC}$,只要证明OC⊥BD即可;
(2)连接BC、作CM⊥AB于M.由$\frac{DC}{AB}$=$\frac{3}{5}$,设BC=DC=3k,则AB=5k,AC=4k,推出OC=$\frac{1}{2}$AB=$\frac{5}{2}$k,由$\frac{1}{2}$•AC•BC=$\frac{1}{2}$•AB•CM,推出CM=$\frac{12}{5}$k,在Rt△OCM中,OM=$\sqrt{O{C}^{2}-C{M}^{2}}$=$\frac{7}{10}$,由sin∠E=sin∠OCM=$\frac{OM}{OC}$,计算即可解决问题.
解答 (1)证明:连接BD、OC.
∵EC是⊙的切线,
∴CO⊥EC,
∵∠ACD=∠ABD=∠E,
∴BD∥EC,
∴BD⊥OC,
∴$\widehat{CD}$=$\widehat{BC}$.
(2)连接BC、作CM⊥AB于M.
∵∠OCM+∠ECM=90°,
∠E+∠ECM=90°,
∴∠OCM=∠E,
∵$\widehat{DC}$=$\widehat{BC}$,
∴CD=BC,
∵$\frac{DC}{AB}$=$\frac{3}{5}$,设BC=DC=3k,则AB=5k,AC=4k,
∴OC=$\frac{1}{2}$AB=$\frac{5}{2}$k,
∵$\frac{1}{2}$•AC•BC=$\frac{1}{2}$•AB•CM,
∴CM=$\frac{12}{5}$k,
在Rt△OCM中,OM=$\sqrt{O{C}^{2}-C{M}^{2}}$=$\frac{7}{10}$,
∴sin∠E=sin∠OCM=$\frac{OM}{OC}$=$\frac{\frac{7}{10}}{\frac{5}{2}}$=$\frac{7}{25}$.
点评 本题考查切线的性质、解直角三角形、锐角三角函数、垂径定理等知识,解题的关键是学会添加常用辅助线,学会利用参数解决问题,学会用转化的思想思考问题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
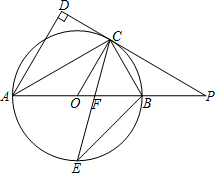 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.
某度假村依山而建,大门A处,有一斜坡AB,长度为13米,在坡顶B处测得度假村楼CF的楼顶C的仰角∠CBF=60?,离B点8米远的E处有一花台,在E处仰望C的仰角∠CEF=73.5°,CF的延长线交校门处的水平面于D点,FD=5米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
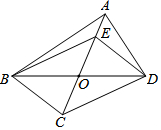 如图,在四边形ABCD中,对角线AC,BD相交于点O,且OB=OD.点E在线段OA上,连结BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是:①②或①④或②④(只填写序号).
如图,在四边形ABCD中,对角线AC,BD相交于点O,且OB=OD.点E在线段OA上,连结BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是:①②或①④或②④(只填写序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
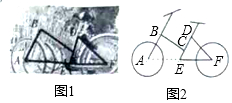 2017年初,合肥市积极推进共享单车服务(如图1),努力创造绿色环保出行,图2是某品牌单车的车架示意图,其中ED=40cm,∠DEF=60°,∠F=45°,求传动轮轴心E到后轮轴心F的距离EF的长.(结果精确到1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
2017年初,合肥市积极推进共享单车服务(如图1),努力创造绿色环保出行,图2是某品牌单车的车架示意图,其中ED=40cm,∠DEF=60°,∠F=45°,求传动轮轴心E到后轮轴心F的距离EF的长.(结果精确到1cm,参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
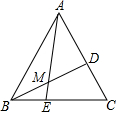 如图,在等边△ABC中,D为AC边上的一点,连接BD,M为BD上一点,且∠AMD=60°,AM交BC于E.当M为BD中点时,$\frac{CD}{AD}$的值为( )
如图,在等边△ABC中,D为AC边上的一点,连接BD,M为BD上一点,且∠AMD=60°,AM交BC于E.当M为BD中点时,$\frac{CD}{AD}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com