
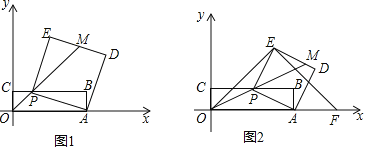
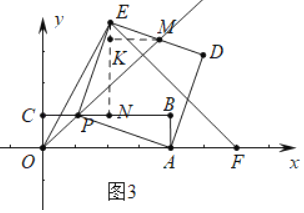
【题目】已知:如图1,矩形OABC的两个顶点A,C分别在x轴,y轴上,点B的坐标是(8,2),点P是边BC上的一个动点,连接AP,以AP为一边朝点B方向作正方形PADE,连接OP并延长与DE交于点M,设CP=a(a>0).
(1)请用含a的代数式表示点P,E的坐标.
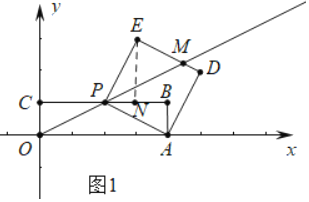
(2)连接OE,并把OE绕点E逆时针方向旋转90°得EF.如图2,若点F恰好落在x轴的正半轴上,求a与![]() 的值.
的值.
(3)①如图1,当点M为DE的中点时,求a的值.
②在①的前提下,并且当a>4时,OP的延长线上存在点Q,使得EQ+![]() PQ有最小值,请直接写出EQ+
PQ有最小值,请直接写出EQ+![]() PQ的最小值.
PQ的最小值.
【答案】(1)P(a,2);E(a+2,10﹣a);(2)a=4,![]() =3;(3)①a=2或6;②
=3;(3)①a=2或6;②![]() .
.
【解析】
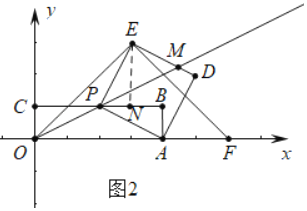
(1)如图1中,作![]() 于N只要证明
于N只要证明![]() ,即可解决问题;
,即可解决问题;
(2)利用等腰直角三角形的性质,根据点E的坐标构建方程求出a,再构建一次函数求出点M坐标,即可解决问题;
(3)①求出点M坐标,根据![]() =
=![]() ,构建方程即可;
,构建方程即可;
②如图4中,将![]() 绕点P顺时针旋转
绕点P顺时针旋转![]() 得到
得到![]() ,则
,则![]() 是等腰直角三角形.可得
是等腰直角三角形.可得![]() 的中点
的中点![]() ,
,![]() ,作
,作![]() ,则
,则![]() ,推出
,推出![]() ,可得当E、Q、R共线时,
,可得当E、Q、R共线时,![]() 的值最小,求出点R坐标即可解决问题;
的值最小,求出点R坐标即可解决问题;
解:(1)如图1中,作![]() 于N.
于N.
∵B![]() ,
,
∴BC=8,![]() ,∵
,∵![]() ,
,
∴![]()
∵四边形OABC是矩形,四边形ADEP是正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.
(2)如图2中,
由题意:△EOF是等腰直角三角形,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴a=4,![]() ,
,
∴直线OP的解析式为![]() ,直线DE的解析式为
,直线DE的解析式为![]() ,
,
由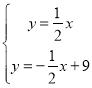 ,解得
,解得![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)①如图3中,作![]() 于K.
于K.
由![]() ,可得,
,可得,![]() ,
,
∴EK=1,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴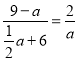 ,
,
整理得:![]() ,
,
解得![]() 或6.
或6.
②如图4中,将![]() 绕点P顺时针旋转
绕点P顺时针旋转![]() 得到
得到![]() ,则
,则![]() 是等腰直角三角形.
是等腰直角三角形.
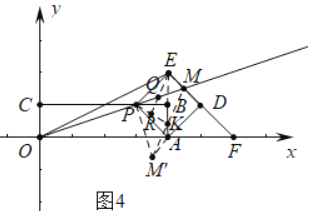
由题意a=6,![]() ,
,
∴![]() 的中点
的中点![]() ,
,
∵![]() ,
,
∴![]() ,作
,作![]() ,则
,则![]() ,
,
∴![]() ,
,
∴当E、Q、R共线时,![]() 的值最小,
的值最小,
∵直线PR的解析式为![]() ,
,
∵![]() ,
,
∴直线ER的解析式为![]() ,
,
由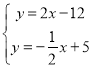 ,解得
,解得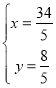 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的最小值为
的最小值为![]() .
.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
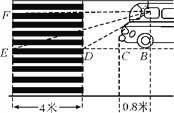
【题目】如图,某小学门口有一直线马路,交警在门口设有一条宽度为4米的斑马线,为安全起见,规定车头距斑马线后端的水平距离不得低于2米,现有一旅游车在路口遇红灯刹车停下,汽车里司机与斑马线前后两端的视角分别为∠FAE=15°和∠FAD=30°,司机距车头的水平距离为0.8米,试问该旅游车停车是否符合上述安全标准?(E,D,C,B四点在平行于斑马线的同一直线上)(参考数据:tan15°=2-![]() ,
,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
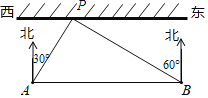
【题目】为了保证端午节龙舟赛在我市侨港海域顺利举办,某部门工作人员乘快艇到侨港海域考察水情,以每秒11米的速度沿平行于岸边的赛道AB由西向东行驶,在A处测得岸边一建筑物P在北偏东30°方向上,继续行驶40秒到达B处时,测得建筑物P在北偏西60°方向上,如图所示,求建筑物P到赛道AB的距离(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
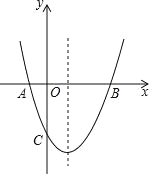
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(A在B的左侧),顶点为C.
(1)求A,B两点的坐标;
(2)若将该抛物线向上平移t个单位后,它与x轴恰好只有一个交点,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元.销售价为每千克60元时,一天能销售80千克,经市场调查,该商品每涨价1元,一天销售量就减少2千克,设该商品的售价涨了x元,每天销售该商品的总利润为y元.
(1)求y与x之间的函数表达式;
(2)当x为多少时每天总利润y最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在2014年至2016年期间销售一种礼盒.2014年,该商店用3500元购进了这种礼盒并且全部售完;2016年,这种礼盒的进价比2014年下降了11元/盒,该商店用2400元购进了与2014年相同数量的礼盒也全部售完,礼盒的售价均为60元/盒.
(1)2014年这种礼盒的进价是多少元/盒?
(2)若该商店每年销售这种礼盒所获利润的年增长率相同,问年增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
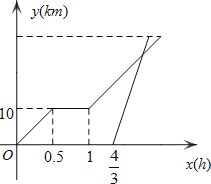
【题目】周末,小明骑自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑车速度的3倍.
(1)求小明骑车的速度和在甲地游玩的时间;
(2)小明从家出发多少小时后被妈妈追上?此时离家多远?
(3)若妈妈比小明早10分钟到达乙地,求从家到乙地的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点。
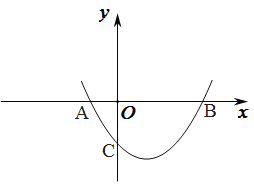
(1)求b、c的值;
(2)P为抛物线上的点,且满足S△PAB=8,求P点的坐标
(3)设抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
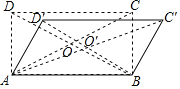
【题目】如图,矩形木框ABCD中,AB=2AD=4,将其按顺时针变形为ABC′D′,当∠AD′B=90°时,四边形对称中心O经过的路径长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com