
如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
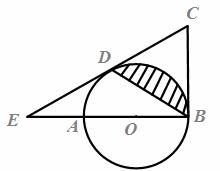
(1)求证:CD为⊙O的切线;
(2)求证:∠C=2∠DBE.
(3)若EA=AO=2,求图中阴影部分的面积.(结果保留π)
(1)证明:连接OD,

∵BC是⊙O的切线,∴∠ABC=90°,
∵CD=CB, ∴∠CBD=∠CDB,
∵OB=OD,∴∠OBD=∠ODB,
∴∠ODC=∠ABC=90°,即OD⊥CD,
∵点D在⊙O上, ∴CD为⊙O的切线.
(2)如图,∠DOE=∠ODB+∠OBD=2∠DBE,分
由(1)得:OD⊥EC于点D,∴∠E+∠C=∠E+∠DOE=90°, ∴∠C=∠DOE=2∠DBE.
(3)作OF⊥DB于点F,连接AD,
由EA=AO可得:AD是Rt△ODE斜边的中线,
∴AD=AO=OD,∴∠DOA=60°,∴∠OBD=30°,
又∵OB=AO=2,OF⊥BD, ∴ OF=1,BF=
∴ OF=1,BF= ,
,
∴BD=2BF=2 ,∠BOD=180°-∠DOA =120°,
,∠BOD=180°-∠DOA =120°,
∴ .…12分
.…12分
注:此大题解法不唯一,请参照给分.


科目:初中数学 来源: 题型:
如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有
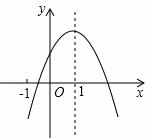
A.①②③ B.①③④ C.③④⑤ D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
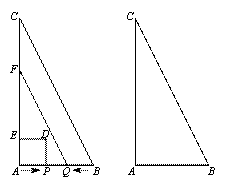
如图,在△ABC中,∠A=90°,AB=2cm,AC=4cm,动点P从点A出发,沿AB方向以1cm/s的速度向点B运动,动点Q从点B同时出发,沿BA方向以1cm/s的速度向点A运动.当点P到达点B时,P,Q两点同时停止运动.以AP为边向上作正方形APDE,过点Q作QF∥BC,交AC于点F.设点P的运动时间为ts,正方形APDE和梯形BCFQ重叠部分的面积为Scm2.
(1)当t=_____s时,点P与点Q重合;
(2)当t=_____s时,点D在QF上;
(3)当点P在Q,B两点之间(不包括Q,B两点)时,
求S与t之间的函数关系式.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
抛物线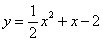 与y轴交于点C,与直线y=x交于A(-2,-2)、B(2,2)两点.如图,线段MN在直线AB上移动,且
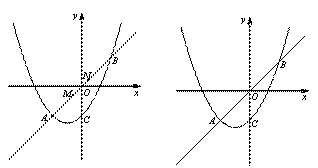
与y轴交于点C,与直线y=x交于A(-2,-2)、B(2,2)两点.如图,线段MN在直线AB上移动,且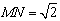 ,若点M的横坐标为m,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以P、M、Q、N为顶点的四边形否为平行四边形?若能,请求出m的值;若不能,请说明理由.
,若点M的横坐标为m,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以P、M、Q、N为顶点的四边形否为平行四边形?若能,请求出m的值;若不能,请说明理由.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
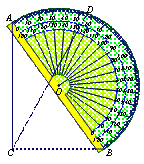
如图,一块直角三角板ABC的斜边AB与量角器的直径重合,点D对应54°,则∠BCD的度数为( )
A. 27° B. 54° C. 63° D. 36°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com