
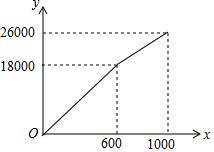
 为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为${y}_{1}=\left\{\begin{array}{l}{{k}_{1}x(0≤x<600)}\\{{k}_{2}x+b(600≤x≤1000)}\end{array}\right.$,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.01x2-20x+30000(0≤x≤1000).
为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为${y}_{1}=\left\{\begin{array}{l}{{k}_{1}x(0≤x<600)}\\{{k}_{2}x+b(600≤x≤1000)}\end{array}\right.$,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.01x2-20x+30000(0≤x≤1000).分析 (1)将x=600、y=18000代入y1=k1x可得k1;将x=600、y=18000和x=1000、y=26000代入y1=k2x+b可得k2、b.
(2)分0≤x<600和600≤x≤1000两种情况,根据“绿化总费用=种草所需总费用+种花所需总费用”结合二次函数的性质可得答案;
(3)根据种草部分的面积不少于700m2,栽花部分的面积不少于100m2求得x的范围,依据二次函数的性质可得.
解答 解:(1)将x=600、y=18000代入y1=k1x,得:18000=600k1,解得:k1=30;
将x=600、y=18000和x=1000、y=26000代入,得:$\left\{\begin{array}{l}{600{k}_{2}+b=18000}\\{1000{k}_{2}+b=26000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=20}\\{b=6000}\end{array}\right.$;
(2)当0≤x<600时,
W=30x+(-0.01x2-20x+30000)=-0.01x2+10x+30000,
∵-0.01<0,W=-0.01(x-500)2+32500,
∴当x=500时,W取得最大值为32500元;
当600≤x≤1000时,
W=20x+6000+(-0.01x2-20x+30000)=-0.01x2+36000,
∵-0.01<0,
∴当600≤x≤1000时,W随x的增大而减小,
∴当x=600时,W取最大值为32400,
∵32400<32500,
∴W取最大值为32500元;
(3)由题意得:1000-x≥100,解得:x≤900,
由x≥700,
则700≤x≤900,
∵当700≤x≤900时,W随x的增大而减小,
∴当x=900时,W取得最小值27900元.
点评 本题主要考查二次函数的应用,掌握待定系数法求函数解析式及分类讨论依据相等关系列出函数解析式是解题的关键.


科目:初中数学 来源: 题型:解答题
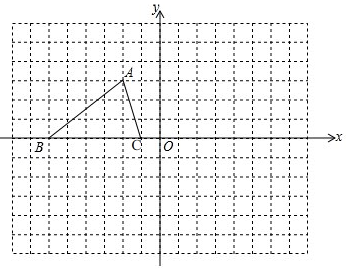 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),已知△ABC三个顶点的坐标分别为A(-2,3)、B(-6,0)、C(-1,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
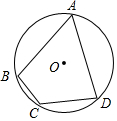 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
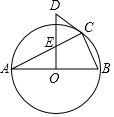 如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
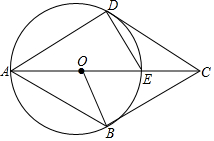 已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D.B点在⊙O上,连接OB.
已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D.B点在⊙O上,连接OB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
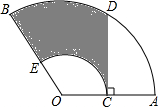 如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与$\widehat{AB}$交于点D,以O为圆心,OC的长为半径作$\widehat{CE}$交OB于点E,若OA=4,∠AOB=120°,则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$.(结果保留π)
如图,在扇形OAB中,C是OA的中点,CD⊥OA,CD与$\widehat{AB}$交于点D,以O为圆心,OC的长为半径作$\widehat{CE}$交OB于点E,若OA=4,∠AOB=120°,则图中阴影部分的面积为$\frac{4}{3}$π+2$\sqrt{3}$.(结果保留π)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com