
【题目】定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
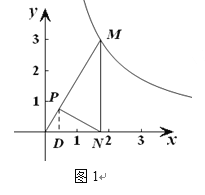
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线C:![]()
![]() 上的任意一点,点N是x轴正半轴上的任意一点.
上的任意一点,点N是x轴正半轴上的任意一点.
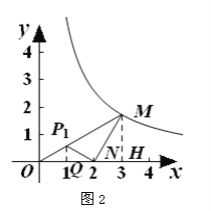
(1) 如图2,点P是OM上一点,∠ONP=∠M, 试说明点P是△MON的自相似点; 当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求点P 的坐标;
时,求点P 的坐标;
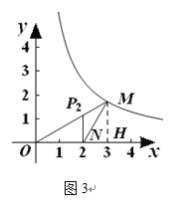
(2) 如图3,当点M的坐标是![]() ,点N的坐标是
,点N的坐标是![]() 时,求△MON的自相似点的坐标;
时,求△MON的自相似点的坐标;
(3) 是否存在点M和点N,使△MON无自相似点,?若存在,请直接写出这两点的坐标;若不存在,请说明理由.



【答案】(1)![]() ;(2)
;(2)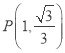 或
或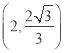 ;(3)存在,
;(3)存在,![]()
【解析】
试题分析:(1)易证点P是三角形MON的自相似点,过点P作PD⊥x轴于D点根据M、N坐标易知∠MNO=90°,再利用三角函数可求出P点坐标![]() ;(2)根据坐标发现ON=MN=2,要找自相似点只能在∠ONM中做∠ONP=∠OMN或∠MNP=∠MON,分别画出图形,根据图形性质,结合相似可求出自相似点的坐标;(3)根据前两问可发现,要想有自相似点,其实质就是在大角里面做小角,当三个角都相等时,即△OMN为等边三角形时,不存在自相似点,因此可得到直线OM的解析式y=
;(2)根据坐标发现ON=MN=2,要找自相似点只能在∠ONM中做∠ONP=∠OMN或∠MNP=∠MON,分别画出图形,根据图形性质,结合相似可求出自相似点的坐标;(3)根据前两问可发现,要想有自相似点,其实质就是在大角里面做小角,当三个角都相等时,即△OMN为等边三角形时,不存在自相似点,因此可得到直线OM的解析式y=![]() x,与
x,与![]() 的交点就是M,从而可以求得N的坐标.
的交点就是M,从而可以求得N的坐标.
试题解析:(1)在△ONP和△OMN中,
∵∠ONP=∠OMN,∠NOP=∠MON
∴△ONP∽△OMN
∴点P是△M0N的自相似点.
过点P作PD⊥x轴于D点.
![]()
∴![]() .
.
∵![]() ,
,
∴![]() , ∴
, ∴![]() .
.
在Rt△OPN中,![]() .
.
![]() .
.
![]() . ∴
. ∴![]() .
.
(2)①如图2,过点M作MH⊥x轴于H点,
∵ ![]() ,
,![]()
∴![]() ,直线OM的表达式为
,直线OM的表达式为![]() .
.![]()
∵![]() 是△M0N的自相似点,∴△
是△M0N的自相似点,∴△![]() ∽△NOM
∽△NOM
过点![]() 作
作![]() ⊥x轴于Q点,
⊥x轴于Q点,
∴![]()
∵![]() 的横坐标为1,∴
的横坐标为1,∴![]() ∴
∴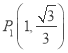 .
.
如图3,△![]() ∽△NOM ,
∽△NOM ,
∴![]() ∴
∴![]() .
.
∵![]() 的纵坐标为
的纵坐标为![]() ,
,
∴![]() ∴
∴![]() ,
,
∴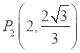 .
.
综上所述,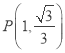 或
或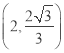 .
.
(3)存在,![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )
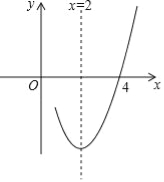
A.①②③ B.③④⑤ C.①②④ D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
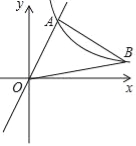
【题目】如图,在平面直角坐标系中,经过点A的双曲线y=![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则k的值为 .
,∠AOB=∠OBA=45°,则k的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【操作发现】
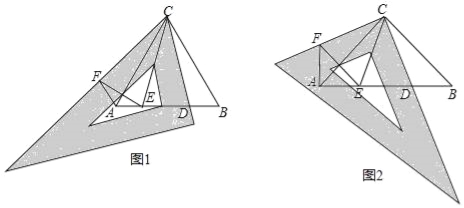
(1)如图1,![]() 为等边三角形,先将三角板中的
为等边三角形,先将三角板中的![]() 角与
角与![]() 重合,再将三角板绕点
重合,再将三角板绕点![]() 按顺时针方向旋转(旋转角大于
按顺时针方向旋转(旋转角大于![]() 且小于
且小于![]() ).旋转后三角板的一直角边与
).旋转后三角板的一直角边与![]() 交于点
交于点![]() .在三角板斜边上取一点
.在三角板斜边上取一点![]() ,使
,使![]() ,线段
,线段![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .
.
①求![]() 的度数;
的度数;
②![]() 与
与![]() 相等吗?请说明理由;
相等吗?请说明理由;
【类比探究】
(2)如图2,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,先将三角板的
,先将三角板的![]() 角与
角与![]() 重合,再将三角板绕点
重合,再将三角板绕点![]() 按顺时针方向旋转(旋转角大于
按顺时针方向旋转(旋转角大于![]() 且小于
且小于![]() ).旋转后三角板的一直角边与
).旋转后三角板的一直角边与![]() 交于点
交于点![]() .在三角板另一直角边上取一点
.在三角板另一直角边上取一点![]() ,使
,使![]() ,线段
,线段![]() 上取点
上取点![]() ,使
,使![]() ,连接
,连接![]() ,
,![]() .请直接写出探究结果:
.请直接写出探究结果:
①![]() 的度数;
的度数;
②线段![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合:
(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数;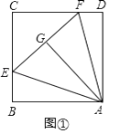
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,BM之间的数量关系,并说明理由.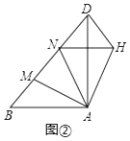
(3)在图①中,连接BD分别交AE,AF于点M,N,若DN=3 ![]() ,BM=3
,BM=3 ![]() ,求MN的长.
,求MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com