

分析 (1)首先求出点B和点C的坐标,然后设抛物线的解析式是y=ax2+bx+c,根据题意列出a,b和c的三元一次方程组,求出a,b和c的值即可;
(2)如图1,过点P作PF⊥y轴于点F,构建全等三角形△PFE≌△BOE(AAS),结合全等三角形的对应边相等和二次函数图象上点的坐标特征来求点P的坐标,则易得BP的长度;
(3)①当以C为直角顶点时,过点C作CP1⊥AC,交抛物线于点P1,过点P1作y轴的垂线,垂足是M,先求出MC=MP1,设P1(m,-m2+3m+4),则m=-m2+3m+4-4,求出m的值即可;②当点A为直角顶点时,过A作AP2⊥AC,交抛物线于点P2,过点P2作y轴的垂线,垂足是N,AP2交y轴于点F.则P2N∥x轴,求出AO=OF,P2N=NF,进而得到m的一元二次方程,求出m的值,即可求出点P的坐标.
解答  解:(1)由A(4,0),可知OA=4,
解:(1)由A(4,0),可知OA=4,
∵OA=OC=4OB,
∴OA=OC=4,OB=1,
∴C(0,4),B(-1,0).
设抛物线的解析式是y=ax2+bx+c,
则$\left\{\begin{array}{l}{a-b+c=0}\\{16a+4b+c=0}\\{c=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-1}\\{b=3}\\{c=4}\end{array}\right.$.
则抛物线的解析式是:y=-x2+3x+4;
(2)如图1,过点P作PF⊥y轴于点F,
∵在△PFE与△BOE中,$\left\{\begin{array}{l}{∠PFE=∠BOE=90°}\\{∠PEF=∠BEO}\\{PE=BE}\end{array}\right.$,
∴△PFE≌△BOE(AAS),
∴PF=OB.
∵B(-1,0),
∴点P的横坐标是1,
把x=1代入y=-x2+3x+4,得
y=-12+3×1+4=6,
故P(1,6),
∴BP=$\sqrt{(-1-1)^{2}+(0-6)^{2}}$=2$\sqrt{10}$;
(3)存在.
第一种情况,如图2,当以C为直角顶点时,过点C作CP1⊥AC,交抛物线于点P1.过点P1作y轴的垂线,垂足是M.
∵∠ACP1=90°,
∴∠MCP1+∠ACO=90°.
∵∠ACO+∠OAC=90°,
∴∠MCP1=∠OAC.
∵OA=OC,
∴∠MCP1=∠OAC=45°,
∴∠MCP1=∠MP1C,
∴MC=MP1,
设P(m,-m2+3m+4),则m=-m2+3m+4-4,
解得:m1=0(舍去),m2=2.
∴-m2+3m+4=6,
即P(2,6).
第二种情况,如图3,当点A为直角顶点时,过A作AP2,AC交抛物线于点P2,过点P2作y轴的垂线,垂足是N,AP交y轴于点F.
∴P2N∥x轴,
由∠CAO=45°,
∴∠OAP=45°,
∴∠FP2N=45°,AO=OF.
∴P2N=NF,
设P2(n,-n2+3n+4),则n=(-n2+3n+4)+4
解得:n1=-2,n2=4(舍去),
∴-n2+3n+4=-6,
则P2的坐标是(-2,-6).
综上所述,P的坐标是(2,6)或(-2,-6).
点评 本题主要考查了二次函数综合题的知识,此题涉及到待定系数法求二次函数解析式、二次函数的性质以及一元二次方程的解法的知识,解答(2)问时,需要作出辅助线,构建全等三角形,解答(3)问需要进行分类讨论,此题有一定的难度.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
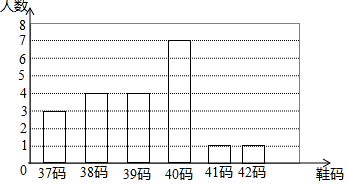 某鞋厂为了了解初中学生穿鞋的鞋号情况,对某中学八年级(1)班的20名男生所穿鞋号进行了调查,结果如图所示
某鞋厂为了了解初中学生穿鞋的鞋号情况,对某中学八年级(1)班的20名男生所穿鞋号进行了调查,结果如图所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,∠ABC=45°,AD是BC边上的中线,过点D作DE⊥AB于点E,且sin∠DAB=$\frac{3}{5}$,DB=3$\sqrt{2}$.求:
已知:如图,在△ABC中,∠ABC=45°,AD是BC边上的中线,过点D作DE⊥AB于点E,且sin∠DAB=$\frac{3}{5}$,DB=3$\sqrt{2}$.求:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.点A与点B之间的距离表示为AB(以下类同).
如图,若点A在数轴上对应的数为a,点B在数轴上对应的数为b,且a,b满足|a+2|+(b-1)2=0.点A与点B之间的距离表示为AB(以下类同).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com