
分析 (1)先根据非负数的性质求出a,b的值,进而得出A,B两点的坐标,根据三角形的面积公式即可得出结论;
(2)分点P在y轴的正半轴上与负半轴上两种情况进行讨论;
(3)先根据直角三角形的性质求出∠ODB的度数,再由DE平分∠ODB得出∠BDE的度数,根据三角形内角和定理求出∠DFB的度数,同理可得出∠EAB的度数,根据AE平分∠CAB可得出∠CAB的度数,进而得出∠C的度数,由此可得出结论.
解答 解:(1)∵(a+2)2+$\sqrt{b-2}$=0,
∴a+2=0,b-2=0,解得a=-2,b=2,
∴A(-2,0),C(2,2),
∴S△ABC=$\frac{1}{2}$AB•BC=$\frac{1}{2}$×4×2=4;
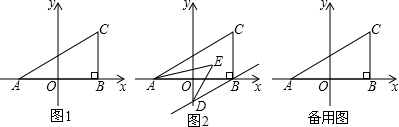
(2)当点P在y轴正半轴上时,如图①设P(0,t),
过点P作MN∥x轴,AN∥y轴,BM∥y轴,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=4,
∴$\frac{4(t-2+t)}{2}$-t-(t-2)=4,解得t=3,
∴P(0,3);
当点P在y轴负半轴上时,如图②设P(0,t),
过点P作MN∥x轴,AN∥y轴,BM∥y轴,
∵S△APC=S梯形MNAC-S△ANP-S△CMP=4,
∴$\frac{4(-t+2-t)}{2}$+t-(2-t)=4,解得t=-1,
∴P(0,-1).
综上所述,P(0,-1)或(0,3).
(3) 设AB与DE交于点F,
设AB与DE交于点F,
∵∠ABD=30°,OB⊥OD,
∴∠ODB=60°,∠CBD=90°+30°=120°,
∵DE平分∠ODB,
∴∠BDE=30°,
∴∠BFD=180°-∠ABD-∠BDE=180°-30°-30°=120°,
∴∠AFE=∠BFD=120°.
∵∠E=45°,
∴∠EAB=180°-120°-45°=15°.
∵AE平分∠CAB,
∴∠CAB=2∠EAB=30°,
∴∠C=90°-30°=60°,
∴∠C+∠CBD=60°+120°=180°,
∴AC∥BD.
点评 本题考查的是坐标与图形性质,熟知三角形的面积公式及非负数的性质是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
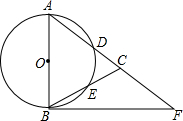 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC延长线上,且∠CBF=$\frac{1}{2}$∠CAB.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC延长线上,且∠CBF=$\frac{1}{2}$∠CAB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com