分析:
(1)延长DM交CE于点N,利用角边角定理可以证明△ADM与△ENM全等,根据全等三角形对应边相等可得DM=MN,AD=NE,再连接DF、FN,根据等腰直角三角形两腰相等,两个底角都是45°,利用边角边定理可以证明△CDF与△ENF全等,根据全等三角形对应边相等可得DF=NF,对应角相等可得∠CFD=∠EFN,然后推出∠DFN=∠CFE=90°,再根据等腰三角形三线合一的性质即可得证;
(2)先过点E作EG∥AD交DC的延长线于点G,然后根据(1)的思路延长DM交EG于点N,利用角边角定理可以证明△ADM与△ENM全等,根据全等三角形对应边相等可得DM=MN,AD=NE,再连接DF、FN,根据四边形的内角和等于360°以及平角等于180°求出∠DCE=∠NEF,再利用边角边定理可以证明△CDF与△ENF全等,根据全等三角形对应边相等可得DF=NF,对应角相等可得∠CFD=∠EFN,然后推出∠DFN=∠CFE=90°,再根据等腰三角形三线合一的性质即可得证。
解答:
(1)证明:如图1,延长DM交CE于点N,
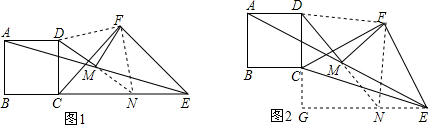
∵M是AE的中点,
∴AM=ME,
∵CE在正方形ABCD的边BC的延长线上,
∴AD∥CE,
∴∠DAM=∠NEM,
在△ADM与△ENM中,∠DAM=∠NEM;AM=EM;∠AMD=∠EMN
∴△ADM≌△ENM(ASA),
∴DM=MN,AD=NE,
连接DF、FN,
∵△CEF是等腰直角三角形,
∴∠CEF=∠ECF=45°,CF=EF,
∴∠DCF=90°-∠ECF=90°-45°=45°,
∴∠CEF=∠DCF,
在△CDF与△ENF中,CD=NE;∠CEF=∠DCF;CF=EF
∴△CDF≌△ENF(SAS),
∴DF=NF,∠CFD=∠EFN,
∵∠CFE=90°,
∴∠DFN=∠CFD+∠CFN=∠EFN+∠CFN=∠CFE=90°,
又∵DM=MN,
∴MD=MF,MD⊥MF(直角三角形斜边上的中线等于斜边的一半,等腰三角形三线合一);
(2)解:仍然成立.理由如下:
如图2,过点E作EG∥AD交DC的延长线于点G,延长DM交EG于点N,
∴∠DAM=∠NEM,
∵M是AE的中点,
∴AM=ME,
在△ADM与△ENM中,∠DAM=∠NEM;AM=EM;∠AMD=∠EMN
∴△ADM≌△ENM(ASA),
∴DM=MN,AD=NE,
连接DF、FN,
∵四边形ABCD是正方形,
∴∠G=∠ADC=90°,
∴∠NEF=360°-90°×2-∠GCF=180°-∠GCF,
∠DCF=180°-∠GCF,
∴∠DCF=∠NEF,
在△CDF与△ENF中,CD=NE;∠DCF=NEF;CF=EF
∴△CDF≌△ENF(SAS),
∴DF=NF,∠CFD=∠EFN,
∵∠CFE=90°,
∴∠DFN=∠CFD+∠CFN=∠EFN+∠CFN=∠CFE=90°,
又∵DM=MN,
∴MD=MF,MD⊥MF(直角三角形斜边上的中线等于斜边的一半,等腰三角形三线合一)。
点评:本题考查了正方形的性质,等腰三角形的性质,全等三角形的判定与性质,等腰三角形三线合一的性质,直角三角形斜边上的中线等于斜边的一半的性质,综合性较强,需要两次利用三角形全等证明,思路比较繁琐。








 与△ABC关于纵轴(
与△ABC关于纵轴( 轴)对称,请你在图5中画出△
轴)对称,请你在图5中画出△ ;
; ,请你在图5中画出△
,请你在图5中画出△ .
.

 当CE= 时,
当CE= 时, .
.