
分析 ①利用两角和与差的正弦函数公式和基本关系式,解方程即可;②利用正弦定理即可得到结论.
解答 解:①∵△ABC中,角A,B,C所对的边分别为a,b,c,cosB=$\frac{\sqrt{3}}{3}$,sin(A+B)=$\frac{\sqrt{6}}{9}$,ac=2$\sqrt{3}$,
∴sinA+$\sqrt{2}$cosA=$\frac{\sqrt{2}}{3}$,
∵sin2A+cos2A=1,
∴27sin2A-6$\sqrt{2}$sinA-16=0,
解得:sinA=$\frac{2\sqrt{2}}{3}$,或sin A=-$\frac{4\sqrt{2}}{9}$(不合题意,舍去),
②由正弦定理得:$\frac{a}{sinA}=\frac{c}{sinC}$∵
sin(A+B)=$\frac{\sqrt{6}}{9}$,
∴a=2$\sqrt{3}$c,
∵ac=2$\sqrt{3}$,
∴c=1.
点评 本题考查了解三角形,三角函数,两角和与差的正弦函数,同角的三角函数的关系,正弦定理,熟练掌握各公式是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
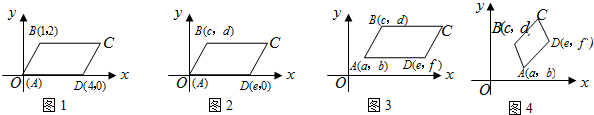
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,△ABC为等腰直角三角形,且AB、BC的长分别是方程x2-10x+m=0的两个根.
如图,在直角坐标系中,△ABC为等腰直角三角形,且AB、BC的长分别是方程x2-10x+m=0的两个根.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )
如图,点C是线段AB上一点,点M是AC的中点,点N是BC的中点,如果MC比NC长2cm,AC比BC长( )| A. | 1cm | B. | 2cm | C. | 4cm | D. | 6cm |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com