
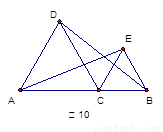
如图10,已知△BCE、△ADC都是等边三角形。求证:AE=BD。(5分)
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011-2012浙江省杭州地区九年级第一学期12月月考数学卷 题型:解答题
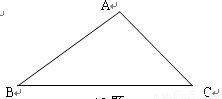
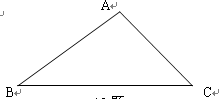
如图10,已知ΔABC.只用直尺(没有刻度的尺)和圆规,求作一个ΔDEF,使得ΔDEF∽ΔABC,且EF=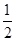 BC.(要求保留作图痕迹,不必写出作法);
BC.(要求保留作图痕迹,不必写出作法);
查看答案和解析>>
科目:初中数学 来源: 题型:
如图10,已知ΔABC.只用直尺(没有刻度的尺)和圆规,求作一个ΔDEF,使得ΔDEF∽ΔABC,且EF=![]() BC.(要求保留作图痕迹,不必写出作法);
BC.(要求保留作图痕迹,不必写出作法);
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com