
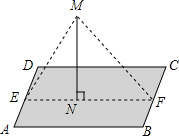
 “五一期间”某公司在一块平行四边形ABCD的湖中,立有一个旗杆MN,MN与湖面垂直,旗杆顶端M与湖岸的E、F两处用绳子相连.绳子上系满了彩旗.且直线EF经过旗杆底部N,EF∥AB,已知,AB=40($\sqrt{3}$+1)m.BC=30m.∠MEN=60°,∠MFN=45°,求绳子EM的长.
“五一期间”某公司在一块平行四边形ABCD的湖中,立有一个旗杆MN,MN与湖面垂直,旗杆顶端M与湖岸的E、F两处用绳子相连.绳子上系满了彩旗.且直线EF经过旗杆底部N,EF∥AB,已知,AB=40($\sqrt{3}$+1)m.BC=30m.∠MEN=60°,∠MFN=45°,求绳子EM的长.  暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
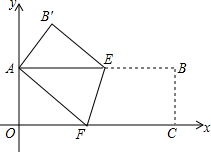 如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标.
如图,矩形纸片AOCB,以点O为坐标原点,分别以矩形的边OC、OA为x轴、y轴建立如图所示的直角坐标系,折叠纸片,使点C与点A重合,点B落在点B′处,折痕为EF,若顶点B的坐标为(9,3),求点E、F、B′的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2017秒时,点P的坐标是(2017,1).
如图,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2017秒时,点P的坐标是(2017,1).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
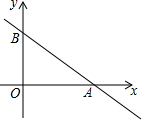 如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.
如图,已知直线y=-$\frac{3}{4}$x+6与x轴、y轴分别交于A、B两点,点C在直线y=-x上,若点D与A,B,C是平行四边形的四个顶点,则线段CD长的最小值为7$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 264×103 | B. | 2.64×104 | C. | 2.64×105 | D. | 0.264×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com