
【题目】已知点![]() (
(![]() ,1)为函数
,1)为函数![]() (
(![]() ,
,![]() 为常数,且
为常数,且![]() )与
)与![]() 的图象的交点.
的图象的交点.
(1)求![]() ;
;
(2)若函数![]() 的图象与
的图象与![]() 轴只有一个交点,求
轴只有一个交点,求![]() ,
,![]() ;
;
(3)若![]() ,设当
,设当![]() 时,函数
时,函数![]() 的最大值为
的最大值为![]() ,最小值为
,最小值为![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)t=1;(2)![]() ,
,![]() 或
或![]() ,
,![]() ;(3)
;(3)![]() 最小值为
最小值为![]()
【解析】
(1)将A(t,1)代入![]() 即可;
即可;
(2)根据题意建立方程组,解出方程组即可得出答案;
(3)根据题意将A(1,1)代入![]() 得出
得出![]() ,然后进一步得到
,然后进一步得到![]() 的对称轴为:
的对称轴为:![]() ,根据
,根据![]() 得到对称轴的范围,然后进一步求解即可.
得到对称轴的范围,然后进一步求解即可.
(1)将A(t,1)代入![]() 得:t=1;
得:t=1;
(2)∵函数![]() 的图象与
的图象与![]() 轴只有一个交点,且过A(1,1),
轴只有一个交点,且过A(1,1),
∴![]() ,且
,且![]() ,
,
∴![]() ,
,![]() 或
或![]() ,
,![]() ;
;
(3)将A(1,1)代入![]() 得:
得:![]() ,
,
即:![]() ,
,
∴![]() ,
,
∴其对称轴为:![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ,
,
∴![]() ≤
≤![]() ≤2,函数图像开口向上,
≤2,函数图像开口向上,
∵![]() ,
,![]() ,
,
∴若![]() 时,
时,![]() 与
与![]() 时的函数值相等,
时的函数值相等,
若![]() ,
,![]() 时的函数值大于
时的函数值大于![]() 时的函数值,
时的函数值,
∴当![]() 时,
时,![]() 的最大值为:
的最大值为:![]() ,
,
![]() 的最小值为:n
的最小值为:n![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴当![]() 时,
时,![]() 最小,最小值为
最小,最小值为![]() ,
,
即![]() 最小值为
最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,BD是⊙O的弦,延长BD到C,使DC=BD,连接AC,过点D作DE⊥AC,垂足为E.
(1)求证:AB=AC;
(2)求证:DE是⊙O的切线;
(3)若⊙O的半径为6,∠BAC=60°,则DE=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在某一个学校的运动俱乐部里面有三大筐数量相同的球,甲每次从第一个大筐中取出9个球;乙每次从第二个大筐中取出7个球;丙则是每次从第三个大筐中取出5个球.到后来甲、乙、丙三人都记不清各自取过多少次球了,于是管理人员查看发现第一个大筐中还剩下7个球,第二个大筐还剩下4个球,第三个大筐还剩下2个球,那么根据上述情况可以推知甲至少取了______次.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 是矩形,点
是矩形,点![]() ,点
,点![]() ,点
,点![]() .以
.以![]() 点为中心,顺时针旋转矩形
点为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]() ,记旋转角为
,记旋转角为![]() .
.
(1)如图①,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
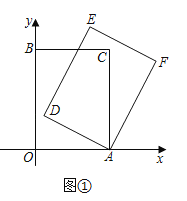
(2)如图②,当点![]() 落在
落在![]() 的延长线上时,求点
的延长线上时,求点![]() 的坐标;
的坐标;

(3)当点![]() 落在线段
落在线段![]() 上时,求点
上时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,
(1)求⊙O的半径;
(2)求O到弦BC的距离.
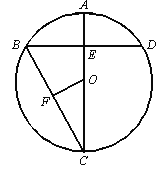
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学一幢教学楼的顶部竖有一块写有“校训”的宣传牌![]() ,
,![]() 米,王老师用测倾器在
米,王老师用测倾器在![]() 点测得
点测得![]() 点的仰角为
点的仰角为![]() ,再向教学楼前进9米到达
,再向教学楼前进9米到达![]() 点,测得点
点,测得点![]() 的仰角为
的仰角为![]() ,若测倾器的高度
,若测倾器的高度![]()
![]()
![]() 米,不考虑其它因素,求教学楼
米,不考虑其它因素,求教学楼![]() 的高度.(结果保留根号)
的高度.(结果保留根号)
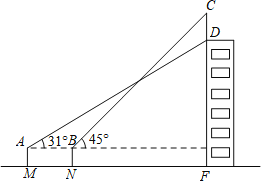
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为R的⊙O的弦AC=BD,AC、BD交于E,F为![]() 上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=
上一点,连AF、BF、AB、AD,下列结论:①AE=BE;②若AC⊥BD,则AD=![]() R;③在②的条件下,若
R;③在②的条件下,若![]() ,AB=
,AB=![]() ,则BF+CE=1.其中正确的是( )
,则BF+CE=1.其中正确的是( )
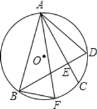
A.①②B.①③C.②③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com