练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

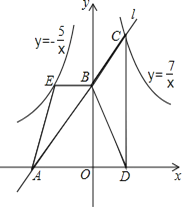
    【题目】如图，在平面直角坐标系xOy中，直线l交x轴和y轴于点A，B，反比例函数y=（x＞0）的图象于点C，过点C作y轴的平行线交x轴于点D，过点B作x轴的平行线交反比例函数y=-（x＜0）的图象于点E，则图中阴影部分的总面积为______．

    【答案】6

    【解析】

    连接OC、OE，由同底等高的三角形面积相等结合反比例函数系数k的几何意义，即可得出S△OBE=S△ABE=×|-5|=2.5、S△OCD=S△BCD=×7=3.5，再将其代入S阴影=S△ABE+S△BCD中，即可求出阴影部分的总面积．

    连接OC、OE，如图所示，

    ∵CD∥y轴，BE∥x轴，

    ∴S△OBE=S△ABE=×|-5|=2.5，

    S△OCD=S△BCD=×7=3.5，

    ∴S阴影=△ABE+S△BCD=2.5+3.5=6，

    故答案为：6．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

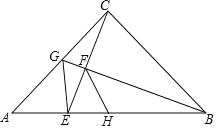
    【题目】如图，△ABC中，∠ACB＝90°，AC＝BC，点G为AC中点，连结BG，CE⊥BG于F，交AB于E，连接GE，点H为AB中点，连接FH．以下结论：（1）∠ACE＝∠ABG；（2）∠AGE＝∠CGB：（3）若AB＝10，则BF＝4；（4）FH平分∠BFE；（5）S△BGC＝3S△CGE．其中正确结论的个数是（　　）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校七年级春游，现有36座和42座两种客车供选择租用，若只租用36座客车若干辆，则正好坐满；若只租用42座客车，则能少租一辆，且有一辆车没有坐满，但超过30人；已知36座客车每辆租金400元，42座客车每辆租金440元.

    （1）该校七年级共有多少人参加春游？

    （2）请你帮该校设计一种最省钱的租车方案.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题的提出:

    如果点P是锐角△ABC内一动点，如何确定一个位置，使点P到△ABC的三顶点的距离之和PA+PB+PC的值为最小?

    问题的转化:

    (1)把ΔAPC绕点A逆时针旋转60度得到连接这样就把确定PA+PB+PC的最小值的问题转化成确定的最小值的问题了,请你利用如图证明:

    ；

    问题的解决:

    (2)当点P到锐角△ABC的三项点的距离之和PA+PB+PC的值为最小时，请你用一定的数量关系刻画此时的点P的位置:_____________________________；

    问题的延伸：

    (3)如图是有一个锐角为30°的直角三角形，如果斜边为2，点P是这个三角形内一动点，请你利用以上方法，求点P到这个三角形各顶点的距离之和的最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，∠B =∠C，点D、E分别是边AB、AC上的点，PD平分∠BDE交BC于H，PE平分∠DEC交BC于G，DQ平分∠ADE交PE延长线于Q。

    （1）∠A+∠B+∠C+∠P +∠Q = °；

    （2）猜想∠P与∠A的数量关系，并证明你的猜想；

    （3）若∠EGH =112°，求∠ADQ 的大小。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，下列能判定AB∥CD的条件有（ ）个．

    （1）∠B+∠BCD=180°；（2）∠1=∠2；（3）∠3=∠4；（4）∠B=∠5．

    A. 1 B. 2 C. 3 D. 4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

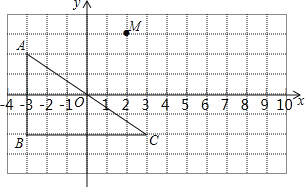
    【题目】如图，已知Rt△ABC的三个顶点分别为A（-3，2），B（-3，-2），C（3，-2）．将△ABC平移，使点A与点M（2，3）重合，得到△MNP．

    （1）将△ABC向 平移 个单位长度，然后再向 平移 个单位长度，可以得到△MNP．

    （2）画出△MNP．

    （3）在（1）的平移过程中，线段AC扫过的面积为 （只需填入数值，不必写单位）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解决问题．

    学校要购买A，B两种型号的足球，按体育器材门市足球销售价格（单价）计算：若买2个A型足球和3个B型足球，则要花费370元，若买3个A型足球和1个B型足球，则要花费240元．

    （1）求A，B两种型号足球的销售价格各是多少元/个？

    （2）学校拟向该体育器材门市购买A，B两种型号的足球共20个，且费用不低于1300元，不超过1500元，则有哪几种购球方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知点，试分别根据下列条件，求出点的坐标。

    （1）点在轴上；

    （2）点横坐标比纵坐标大3；

    （3）点在过点，且与轴平行的直线上。

    查看答案和解析>>

    同步练习册答案