
【题目】如图(1),在Rt△ABC中,∠A=90°,AC=AB=4,D,E分别是AB,AC的中点.若等腰Rt△ADE绕点A逆时针旋转,得到等腰Rt△AD1E1,如图(2),设旋转角为α(0<α≤180°),记直线BD1与CE1的交点为P.
(1)求证:BD1=CE1;(2)当∠CPD1=2∠CAD1时,求CE1的长;
(3)连接PA,△PAB面积的最大值为 .(直接填写结果)

【答案】(1)证明见解析(2)![]() (3)2+2
(3)2+2![]()
【解析】试题分析:(1)先求证AC=AB,再由中点可得出结果;
(2)由(1)的结论,在利用勾股定理计算即可;
(3)作出辅助线,利用勾股定理建立方程求出即可.
试题解析:
(1)∵∠A=90°,∠B=45°,
∴∠C=45°,
∴∠C=∠B ,
∴AC=AB,
∵D,E分别是AB,AC的中点 ,
∴CE= ![]() AC, BD=
AC, BD=![]() AB
AB
∴BD= CE
(2)由(1)知△ABD1≌△ACE1,可证∠CPD1=90°,
∴∠CAD1=45°,∠BAD1=135°
在△ABD1中,可以求得BD12=20+8![]()
∴CE12=20+8![]()
(3) 作PG⊥AB,交AB所在直线于点G,如图
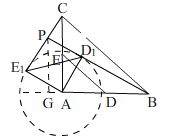
∵D1,E1在以A为圆心,AD为半径的圆上,
当BD1所在直线与⊙A相切时,直线BD1与CE1的交点P到直线AB的距离最大,
此时四边形AD1PE1是正方形,PD1=2,
则BD1=![]()
∴∠ABP=30°,
∴PB=2+![]()
∴点P到AB所在直线的距离的最大值为:PG=1+![]() ,
,
∴△PAB的面积最大值为![]() AB×PG=2+
AB×PG=2+![]() .
.
故答案是:2+![]() .
.


科目:初中数学 来源: 题型:
【题目】我们知道,一元二次方程x2=-1没有实数根,即不存在一个实数的平方等于-1.若我们规定一个新数“i”,使其满足i2=-1(即方程x2=-1有一个根为i).并且进一步规定:一切实数可以与新数进行四则运算,且原有运算律和运算法则仍然成立,于是有i1=i,i2=-1,i3=i2i=(-1)i=-i,i4=(i2)2=(-1)2=1,从而对于任意正整数n,我们可以得到i4n+1=i4ni=(i4)ni=i,同理可得i4n+2=-1,i4n+3=-i,i4n=1.那么i+i2+i3+i4+…+i2015+i2016+i2017的值为 _______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要调查下列问题,你觉得应用全面调查的是( )
A. 检测某城市的空气质量
B. 了解全国中学生的视力和用眼卫生情况
C. 企业招聘,对应聘人员进行面试
D. 调查某池塘中现有鱼的数量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数![]() (
(![]() 为正常数)的图象与
为正常数)的图象与![]() 轴交于A、B两点(A在B的左侧),与
轴交于A、B两点(A在B的左侧),与![]() 轴交于C点.直线
轴交于C点.直线![]() 过M(0,m)(
过M(0,m)(![]() 且
且![]() )且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数
)且与x轴平行,并与直线AC、BC分别相交于点D、E.二次函数![]() 的图象关于直线
的图象关于直线![]() 的对称图象与y轴交于点P.设直线PD与
的对称图象与y轴交于点P.设直线PD与![]() 轴交点为Q ,则:
轴交点为Q ,则:
⑴ 求A、C两点的坐标;
⑵ 求![]() 的值(用含m的代数式表示);
的值(用含m的代数式表示);
⑶ 是否存在实数m,使![]() ?若能,则求出相应的m的值;若不能,请说明理由.
?若能,则求出相应的m的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P到x轴的距离为2,到y轴的距离为3,且点P在x轴的上方,则点P的坐标为( )
A. (2,3)B. (3,2)
C. (2,3)或(-2,3)D. (3,2)或(-3,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,AB=14,BC=15,AC=13
(1) sinB=_________,△ABC的面积为_________
(2) 如图2,点P由B点出发,以1个单位/s的速度向C点运动,过P作PE∥AB、PD∥AC分别交AC、AB边于E、D点,设运动时间为t秒
① 是否存在唯一的t值,使四边形PEAD的面积为S?若存在,求S值;若不存在,说明理由
② 如图3,将△PDE沿DE折叠至△QDE位置,连BQ、CQ,当t为何值时,2BQ=CQ



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知函数y=![]() 和函数y=
和函数y=![]() x+1的图象交于A,B两点,点A的坐标为(2,2),以下结论:①反比例函数的图象一定过点(-1,-4);②当x>2时,
x+1的图象交于A,B两点,点A的坐标为(2,2),以下结论:①反比例函数的图象一定过点(-1,-4);②当x>2时, ![]() x+1>
x+1>![]() ;③点B的坐标是(-4,-1);④S△OCD=1,其中正确结论的个数是( )
;③点B的坐标是(-4,-1);④S△OCD=1,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com