
分析 (1)直接利用待定系数法求出一次函数解析式进而得出答案;
(2)首先表示出每天的获利,进而利用配方法结合二次函数增减性得出答案.
解答 解:(1)当x=25时,y=2000÷(25-15)=200(千克),
设y与x的函数关系式为:y=kx+b,
把(20,250),(25,200)代入得:
$\left\{\begin{array}{l}{20k+b=250}\\{25k+b=200}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-10}\\{b=450}\end{array}\right.$,
∴y与x的函数关系式为:y=-10x+450;
(2)设每天获利W元,
W=(x-15)(-10x+450)
=-10x2+600x-6750
=-10(x-30)2+2250,
∵a=-10<0,
∴开口向下,
∵对称轴为x=30,
∴在x≤28时,W随x的增大而增大,
∴x=28时,W最大值=13×170=2210(元),
答:售价为28元时,每天获利最大为2210元.
点评 此题主要考查了二次函数的应用以及一次函数应用,正确利用二次函数增减性分析是解题关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
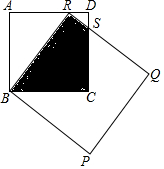 如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD、BPQR的面积分别为16、25,则四边形RBCS的面积为何( )
如图为两正方形ABCD,BPQR重叠的情形,其中R点在AD上,CD与QR相交于S点.若两正方形ABCD、BPQR的面积分别为16、25,则四边形RBCS的面积为何( )| A. | 8 | B. | $\frac{17}{2}$ | C. | $\frac{28}{3}$ | D. | $\frac{77}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
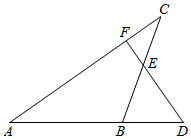 如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )
如图,△ABC的边AB的延长线上有一个点D,过点D作DF⊥AC于F,交BC于E,且BD=BE,则以下结论正确的是( )| A. | ∠FEC=45° | B. | BE=DE | C. | AB=BC | D. | AB=DF |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
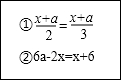 数学老师在如图所示的木板上写了关于x的两个方程,并解出方程①的解比方程②的解小4,则a的值为( )
数学老师在如图所示的木板上写了关于x的两个方程,并解出方程①的解比方程②的解小4,则a的值为( )| A. | $\frac{3}{2}$ | B. | $-\frac{3}{2}$ | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com