小刚在学习绝对值的时候发现:|3-1|可表示数轴上3和1这两点间的距离;而|3+1|即|3-(-1)|则表示3和-1这两点间的距离.根据上面的发现,小刚将|x-2|看成x与2这两点在数轴上的距离;那么|x+3|可看成x与______在数轴上的距离.小刚继续研究发现:x取不同的值时,|x-2|+|x+3|=5有最 值,请你借助数轴解决下列问题
(1)当|x-2|+|x+3|=5时,x可取整数______(写出一个符合条件的整数即可);
(2)若A=|x+1|+|x-5|,那么A的最小值是______;
(3)若B=|x+2|+|x|+|x-1|,那么B的最小值是______,此时x为______;
(4)写出|x+5|+|x+3|+|x+1|+|x-2|的最小值.
解:∵|x+3|=|x-(-3)|,
∴|x+3|可看成x与-3的点在数轴上的距离;
(1)x=0时,|x-2|+|x+3|=|-2|+|3|=2+3=5;
(2)|x+1|+|x-5|表示x到点-1与到点5的距离之和,
当-1≤x≤5时,A有最小值,即表示数5的点到表示数-1的点的距离,所以A的最小值为6;
(3)|x+2|+|x|+|x-1|表示x到数-2、0、1三点的距离之和,
所以当x=0时,它们的距离之和最小,
即B的最小值为3,此时x=0;
(4)|x+5|+|x+3|+|x+1|+|x-2|表示x到数-5、-3、-1、2四点的距离之和,
所以当-3≤x≤-1时,它们的距离之和有最小值9,即|x+5|+|x+3|+|x+1|+|x-2|的最小值为9.
分析:根据绝对值的几何意义得到|x+3|可看成x与-3的点在数轴上的距离;
(1)当-3≤x≤2时,|x-2|+|x+3|=5,然后在次范围内写一整数即可;
(2)由于|x+1|+|x-5|表示x到点-1与到点5的距离之和,然后在-1≤x≤5范围内取一x的值代入可得到A的最小值;
(3)由于|x+2|+|x|+|x-1|表示x到数-2、0、1三点的距离之和,则当x=0时,B有最小值;
(4)由于|x+5|+|x+3|+|x+1|+|x-2|表示x到数-5、-3、-1、2四点的距离之和,在-3≤x≤-1范围内任取一x的值代入计算可得到|x+5|+|x+3|+|x+1|+|x-2|的最小值.
点评:本题考查了绝对值:若a>0,则|a|=a;若a=0,则|a|=0;若a<0,则|a|=-a.也考查了数轴.



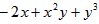 是三次三项式。”
是三次三项式。”