
如图(1),我们将相同的两块含30°角的直角三角尺Rt△DEF与Rt△ABC叠合,使DE在AB上,DF过点C,已知AC=DE=6。将图(1)中的△DEF绕点D逆时针旋转(DF与AB不重合),使边DF、DE分别交AC、BC于点P、Q,如图(2)。
(1)求证:△CQD∽△APD
(2)连结PQ,设AP=x,求面积S△PCQ 关于x的函数关系式;
(3)将图(1)中的△DEF 向左平移(A、D不重合),使边FD、FE分别交AC、BC于点M、N,如图(3),连结MN,试问△MCN面积是否存在最大值、如不存在,请说明理由;如存在请求出S△MCN 的最大值,

(1)∵∠F=∠B=30°,∠ACB=∠BDF=90°
∴∠BCD=∠A=60°,
∵∠ADP+∠PDC=90°,∠CDE+∠PDC=90°
∴△CQD∽△APD
(2)∵在Rt△ADC中,AD=3,DC=3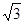
又∵△CQD∽△APD,CQ=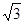 x.
x.
∴S△PCQ=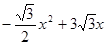
(3)△BEN是等腰三角形.BE=6-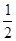 t,BN=
t,BN=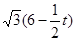 .
.
S△MCN=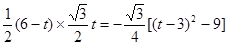
S△MCN 的最大值为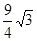
【解析】(1)易得∠BCD=∠A=60°,∠ADP=∠CDE,那么可得△CQD∽△APD;
(2)利用相似可得CQ=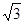 x,那么PC=6-x.可表示出S△PCQ;
x,那么PC=6-x.可表示出S△PCQ;
(3)由外角∠FEN=60°,∠B=30°,可得∠BNE=30°,∴NE=BN,那么△BEN是等腰三角形.易得AD=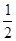 t,AB=12,那么BE=12-AD-DE=6-
t,AB=12,那么BE=12-AD-DE=6-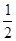 t.过E作EG⊥BN于点G.利用30°的三角函数可求得BG,进而求得BN,然后利用t表示出MC、CN,即可表示出所求面积,再求出S△MCN 的最大值。
t.过E作EG⊥BN于点G.利用30°的三角函数可求得BG,进而求得BN,然后利用t表示出MC、CN,即可表示出所求面积,再求出S△MCN 的最大值。


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
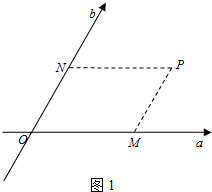 如图1,在平面内取一点O,过点O作两条夹角为60°的数轴,使它们以点O为公共原点且具有相同的单位长度,这样在平面内建立的坐标系称为斜坐标系,我们把水平放置的数轴称为横轴(记作a轴),将斜向放置的数轴称为斜轴(记作b轴).类似
如图1,在平面内取一点O,过点O作两条夹角为60°的数轴,使它们以点O为公共原点且具有相同的单位长度,这样在平面内建立的坐标系称为斜坐标系,我们把水平放置的数轴称为横轴(记作a轴),将斜向放置的数轴称为斜轴(记作b轴).类似

查看答案和解析>>
科目:初中数学 来源: 题型:
 14、相传古印度一座梵塔圣殿中,铸有一片巨大的黄铜板,之上树立了三米高的宝石柱,其中一根宝石柱上插有中心有孔的64枚大小两两相异的一寸厚的金盘,小盘压着较大的盘子,如图,把这些金盘全部一个一个地从1柱移到3柱上去,移动过程不许以大盘压小盘,不得把盘子放到柱子之外.移动之日,喜马拉雅山将变成一座金山.
14、相传古印度一座梵塔圣殿中,铸有一片巨大的黄铜板,之上树立了三米高的宝石柱,其中一根宝石柱上插有中心有孔的64枚大小两两相异的一寸厚的金盘,小盘压着较大的盘子,如图,把这些金盘全部一个一个地从1柱移到3柱上去,移动过程不许以大盘压小盘,不得把盘子放到柱子之外.移动之日,喜马拉雅山将变成一座金山.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 1 | 4 |
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(山东淄博卷)数学 题型:选择题
相传古印度一座梵塔圣殿中,铸有一片巨大的黄铜板,之上树立了三米高的宝石柱,其中一根宝石柱上插有中心有孔的64枚大小两两相异的一寸厚的金盘,小盘压着较大的盘子,如图,把这些金盘全部一个一个地从1柱移到3柱上去,移动过程不许以大盘压小盘,不得把盘子放到柱子之外。移动之日,喜马拉雅山将变成一座金山。

设h(n) 是把n个盘子从1柱移到3柱过程中移动盘子知最少次数
n=1时,h(1)=1
 n=2时,小盘 2柱,大盘 3柱,小柱从2柱 3柱,完成。即h(2)=3
n=2时,小盘 2柱,大盘 3柱,小柱从2柱 3柱,完成。即h(2)=3

 n=3时,小盘 3柱,中盘 2柱,小柱从3柱 2柱。 [即用h(2)
n=3时,小盘 3柱,中盘 2柱,小柱从3柱 2柱。 [即用h(2)
方法把中、小两盘移到2柱,大盘3柱;再用h(2)种方法把中、小两盘从2柱3柱,完成
我们没有时间去移64个盘子,但你可由以上移动过程的规律,计算n=6时, h(6)=
A.11 B.31 C.63 D.127
查看答案和解析>>
科目:初中数学 来源:2011年广西百色市中考数学试卷(解析版) 题型:选择题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com