
如图,已知正方形B的面积为144,正方形C的面积为169时,那么正方形A的面积为( )
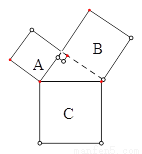
A. 313 B. 144 C. 169 D. 25
D 【解析】设三个正方形的边长依次为,由于三个正方形的三边组成一个直角三角形,所以,故,即. 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:解答题
如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:单选题
甲、乙两人同时从A地出发,骑自行车行30千米到B地,甲比乙每小时少走3千米,结果乙先到40分钟。若设乙每小时走x千米,则可列方程( )
A.  B.
B. 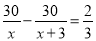 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:填空题
如图,从点A(0,2)发出一束光,经x轴反射,过点B(4,3),则这束光从点A到点B所经过的路径的长为_____.

查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十七章达标检测卷 题型:单选题
如图,一圆柱高8 cm,底面半径为 cm,一只蚂蚁从点
cm,一只蚂蚁从点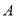 爬到点
爬到点 处吃食,要爬行的最短路程是( )cm.
处吃食,要爬行的最短路程是( )cm.

A. 6 B. 8 C. 10 D. 12
C 【解析】【解析】 底面圆周长为2πr,底面半圆弧长为πr,即半圆弧长为: ×2π×=6(cm),展开后的图形中,有BC=8cm,AC=6cm,根据勾股定理得:AB==10(cm).故选C.查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:解答题
一名男生推铅球,铅球行进的高度y(单位:m)与水平距离x(单位:m)之间的关系是 .
.
(1)铅球行进的最大高度是多少?
(2)该男生把铅球推出的水平距离是多少?
(3)铅球在下落的过程中,行进高度由 m变为
m变为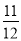 m时,铅球行进的水平距离是多少?
m时,铅球行进的水平距离是多少?
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,BC= ,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__________(结果保留π).
,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__________(结果保留π).

查看答案和解析>>
科目:初中数学 来源:2017-2018学年北师大版七年级数学上册:第5章 一元一次方程 单元测试卷 题型:解答题
如图,线段AB=60厘米.
(1)点P沿线段AB自A点向B点以4厘米/分的速度运动,同时点Q沿线段自B点向A点以6厘米/分的速度运动,几分钟后,P、Q两点相遇?
(2)几分钟后,P、Q两点相距20厘米?

查看答案和解析>>
科目:初中数学 来源:山西省吕梁市孝义市2016-2017学年九年级(上)期末考试数学试卷 题型:单选题
将抛物线y= x2+1向左平移2个单位,再向下平移3个单位,得到的抛物线的函数表达式为( )
x2+1向左平移2个单位,再向下平移3个单位,得到的抛物线的函数表达式为( )
A. y= (x﹣2)2+4 B. y=
(x﹣2)2+4 B. y=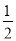 (x﹣2)2﹣2
(x﹣2)2﹣2
C. y= (x+2)2+4 D. y=
(x+2)2+4 D. y= (x+2)2﹣2
(x+2)2﹣2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com