
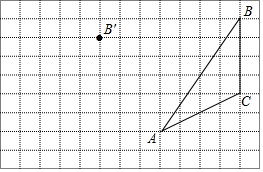
 如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.
如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题. 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:解答题
| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
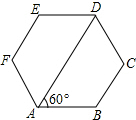 如图,六边形ABCDEF的各个内角都相等,且∠DAB=60°.
如图,六边形ABCDEF的各个内角都相等,且∠DAB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
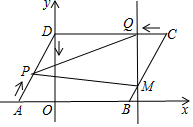 如图,已知平行四边形ABCD,AD=5,A(-3,0),B(6,0),点D在y轴的正半轴上,动点P从点A出发,沿A-D-O的折线以每秒1个单位的速度匀速运动,动点Q同时从点C出发,沿C-D以每秒1个单位的速度匀速运动,过动点Q的直线L始终与 x轴垂直且与折线CBO交于点M,点P、Q中有一个点到达终点,另一个点运动随即而停止.当△PMQ为等腰三角形时,t(t≥5)的值为5s或7s或(9-2$\sqrt{2}$)s.
如图,已知平行四边形ABCD,AD=5,A(-3,0),B(6,0),点D在y轴的正半轴上,动点P从点A出发,沿A-D-O的折线以每秒1个单位的速度匀速运动,动点Q同时从点C出发,沿C-D以每秒1个单位的速度匀速运动,过动点Q的直线L始终与 x轴垂直且与折线CBO交于点M,点P、Q中有一个点到达终点,另一个点运动随即而停止.当△PMQ为等腰三角形时,t(t≥5)的值为5s或7s或(9-2$\sqrt{2}$)s.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com