
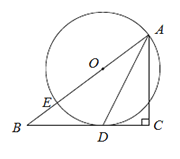
【题目】已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD.
(1)求证:AD是∠BAC的平分线;
(2)若AC=3,BC=4,求⊙O的半径.
【答案】(1)证明见解析(2)![]()
【解析】试题分析:
(1)连接OD,由⊙O与BC边相切于点D可得∠ODB=∠C=90°,从而可得OD∥AC,由此即可得到∠CAD=∠ADO,由OD=OA可得∠DAO=∠ODA,即可得到∠CAD=∠DAO,从而得到AD是∠BAC的角平分线;
(2)在Rt△ABC中,由AC=3,BC=4易得AB=5,由tanB=![]() ,设OD=3x,则BD=4x,由此在Rt△OBD中可得OB=5x,结合OA=OD=3x可得AB=8x=5,解得x=
,设OD=3x,则BD=4x,由此在Rt△OBD中可得OB=5x,结合OA=OD=3x可得AB=8x=5,解得x=![]() ,即可得到⊙O的半径为:
,即可得到⊙O的半径为: ![]() .
.
试题分析:
(1)如图,连接OD,
∵⊙O与BC边相切于点D,
∴∠ODB=∠C=90°,
∴OD∥AC,
∴∠CAD=∠ADO,
∵OD=OA,
∴∠DAO=∠ODA,
∴∠CAD=∠DAO,
∴AD是∠BAC的角平分线;
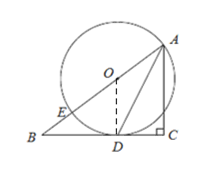
(2)∵在Rt△ABC中,由AC=3,BC=4,
∴AB=![]() ,
,
∵tanB=![]() ,
,
∴可设OD=3x,则BD=4x,
∴OB=![]() ,
,
又∵OA=OD=3x,
∴AB=3x+5x=8x=5,解得:x=![]() ,
,
∴⊙O的半径OD=3x=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,把长方形纸片ABCD沿EF折叠后.点D与点B重合,点C落在点C′的位置上.若∠1=60°,AE=1.
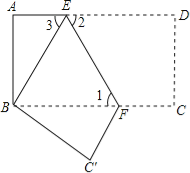
(1)求∠2、∠3的度数;
(2)求长方形纸片ABCD的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”是“丝绸之路经济带”和“21世纪海上丝绸之路”的简称.旨在借用古代丝绸之路的历史符号,高举和平发展的旗帜,积极发展与沿线国家的经济合作.2018年底共开行中欧班列6300列,其中返程班列2690列,实现进出口贸易总额170亿美元.数据170亿用科学计数法表示为![]() ,则
,则![]() 的值为( )
的值为( )
A.9B.10C.11D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有两个点![]() ,
,![]() .
.
(1)若![]() 、
、![]() 关于
关于![]() 轴对称,则
轴对称,则![]() _________________,
_________________,![]() ________________.
________________.
(2)若![]() 、
、![]() 关于
关于![]() 轴对称,则
轴对称,则![]() _________________,
_________________,![]() ________________.
________________.
(3)若![]() 、
、![]() 两点重合,将重合后的点绕原点顺时针旋转
两点重合,将重合后的点绕原点顺时针旋转![]() ,此时点的坐标为__________.
,此时点的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个三位数,十位上的数字是百位上数字的2倍,十位上的数字比个位上的数字大1.
(1)若设百位上的数字为a,则个位数字为 ,这个三位数可表示为 ;
(2)这个三位数能被5整除吗?若能,求出这个三位数;若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广节能灯,为响应号召,某商场计划购进甲、乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲 | 25 | 30 |
乙 | 45 | 60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由边长为1的小正方形组成的格点中,建立如图平面直角坐标系,△ABC的三个顶点坐标分别为A(2,1),B(4,5),C(5,2).
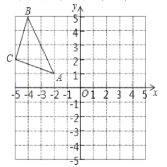
(1)请画出△ABC关于y轴对称的△A![]() B
B![]() C
C![]() ;
;
(2)画出△ABC关于原点O成中心对称的△A![]() B
B![]() C
C![]() ;
;
(3)请你判断△AA![]() A
A![]() 与△CC
与△CC![]() C
C![]() 的相似比;若不相似,请直接写出△AA
的相似比;若不相似,请直接写出△AA![]() A
A![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 轴上,已知点
轴上,已知点![]() 的坐标为
的坐标为![]() ,且
,且![]() .
.
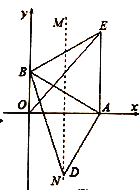
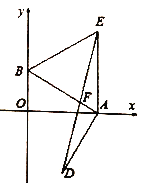
(1) (2) (3)
(1)求![]() 的长度;
的长度;
(2)以![]() 为一边作等边,过点
为一边作等边,过点![]() 作
作![]() ,交
,交![]() 的垂直平分线
的垂直平分线![]() 于点
于点![]() .求证:
.求证:![]() ;
;
(3)在(2)的条件下,连接![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() 为
为![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与双曲线![]() 相交于点A(m,3),B(-6,n),与x轴交于点C.
相交于点A(m,3),B(-6,n),与x轴交于点C.
(1)求直线y=kx+b(k≠0)的解析式;
(2)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标(直接写出结果).
S△BOC,求点P的坐标(直接写出结果).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com