
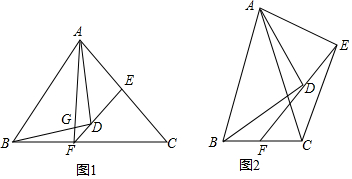
分析 (1)①如图1,连接CD,根据DE是AC的中垂线,得AD=DC,则∠DAC=∠ACD,所以∠DBC=∠DCB,根据三角形的内角和得:2∠ACD+2∠DCB=90°,则∠ACD+∠DCB=45°,从而得出结论;
②如图2,如图2,由AF=FC得$\frac{BF}{AF}=\frac{2}{3}$,过G作GH⊥AB于H,利用同角的三角函数得:tan∠BAF=$\frac{BF}{AF}$=$\frac{GH}{AH}=\frac{2}{3}$,设GH=2x,AH=3x,则AG=$\sqrt{13}$x,计算AF的长,得FG的长,最后计算线段AG:GF的值即可;
(2)如图3,作辅助线,构建全等三角形,证明△BDM≌△CED和△BNM≌△CFD,得BC=2+2=4,再证明△ADE∽△ABC,列比例式可得结论.
解答 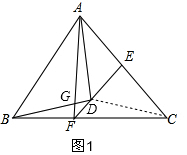 证明:(1)①连接CD,
证明:(1)①连接CD,
∵AE=EC,EF⊥AC,
∴DE是AC的中垂线,
∴AD=DC,
∴∠DAC=∠ACD,
∵AD=BD,
∴BD=CD,
∴∠DBC=∠DCB,
∵∠ADB=90°,
∴△ADB是直角三角形,
∴∠DAB=∠DBA=45°,
∴∠DAB+∠DBA=90°,
∴2∠ACD+2∠DCB=90°,
∴∠ACD+∠DCB=45°,
即∠ACB=45°;
②如图2,∵AE=EC,EF⊥BC,
∴AF=FC,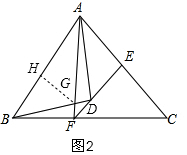
∵BF:CF=2:3,
∴$\frac{BF}{AF}=\frac{2}{3}$,
∵∠FEC=90°,∠ACB=45°,
∴∠EFC=45°,
∴EF=EC,
∴EF=EC=AE,
∴△AEF是等腰直角三角形,
∴∠AFE=45°,
∴∠AFC=45°+45°=90°,
∴△ABF是直角三角形,
过G作GH⊥AB于H,
∴tan∠BAF=$\frac{BF}{AF}$=$\frac{GH}{AH}=\frac{2}{3}$,
设GH=2x,AH=3x,则AG=$\sqrt{13}$x,
∵△ADB是等腰直角三角形,
∴∠ABD=45,
∴△BHG是等腰直角三角形,
∴BH=GH=2x,
∴AB=2x+3x=5x,
cos∠BAF=$\frac{AF}{AB}=\frac{AH}{AG}$,
∴$\frac{AF}{5x}=\frac{3x}{\sqrt{13}x}$,
∴AF=$\frac{15\sqrt{13}}{13}$x,
∴FG=AF-AG=$\frac{15\sqrt{13}}{13}$x-$\sqrt{13}$x=$\frac{2\sqrt{13}}{13}$x,
∴AG:GF=$\sqrt{13}$x:$\frac{2\sqrt{13}}{13}$x=13:2;
(2)如图3,在DF上取一点M,使DM=DE=3,连接BM、DC,
由旋转得:BD=CE,AD=AE,∠ADB=∠AEC=90°,
∴∠ADE+∠BDF=∠AEF+∠FEC=90°,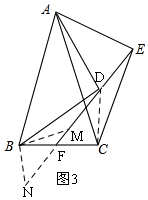
∵AD=AE,
∴∠ADE=∠AEF,
∴∠BDF=∠FEC,
∴△BDM≌△CED(SAS),
∴∠BMD=∠CDE,BM=CD,
∴∠BMF=∠FDC,
延长EF至N,使FN=DE=3,连接BN,
∴FN=DM,
∴FN+FM=DM+FM,
即MN=FD,
∴△BNM≌△CFD,
∴∠DFC=∠N=∠BFN,
∴BF=BN=2,
∴FC=BN=2,
∴BC=2+2=4,
∵∠BAD=∠CAE,
∴∠BAD-∠CAD=∠CAE-∠CAD,
即∠BAC=∠DAE,
∵AB=AC,AD=AE,
∴∠ABC=∠ACB,∠ADE=∠AED,
∴∠ADE=∠ABC,
∴△ADE∽△ABC,
∴$\frac{AD}{AB}=\frac{DE}{BC}=\frac{3}{4}$,
在Rt△ABD中,sin∠ABD=$\frac{AD}{AB}=\frac{3}{4}$.
点评 本题是三角形的综合题,考查了三角形全等的性质和判定,三角形相似的性质和判定、三角函数、线段垂直平分线的性质、等腰直角三角形的性质和判定,第一问利用比的份数设未知数,求线段的比;第二问作辅助线构建全等三角形是关键,难度适中.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:填空题
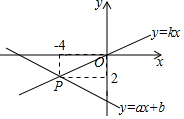 如图,已知函数y=ax+b(a,b为常数,且a≠0)和y=kx(k为常数,且k≠0)
如图,已知函数y=ax+b(a,b为常数,且a≠0)和y=kx(k为常数,且k≠0)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
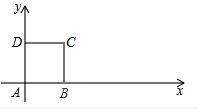 如图,在平面直角坐标系中放置一个边长为1的正方形ABCD,将其沿x轴的正方向无滑动地在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径与x轴围成的面积为( )
如图,在平面直角坐标系中放置一个边长为1的正方形ABCD,将其沿x轴的正方向无滑动地在x轴上滚动,当点A离开原点后第一次落在x轴上时,点A运动的路径与x轴围成的面积为( )| A. | $\frac{π}{2}$+$\frac{1}{2}$ | B. | $\frac{π}{2}$+1 | C. | π+$\frac{1}{2}$ | D. | π+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 普通(元/间/天) | 豪华(元/间/天) | |
| 三人间 | 240 | 500 |
| 双人间 | 180 | 420 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com