
 如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为9.
如图,在△ABC中,AB=3,AC=6,将△ABC绕点C按逆时针方向旋转得到△A1B1C,使CB1∥AD,分别延长AB、CA1相交于点D,则线段BD的长为9. 分析 利用平行线的性质以及旋转的性质得出△CAD∽△B′A′C,再利用相似三角形的性质得出AD的长,进而得出BD的长.
解答 解:∵将△ABC绕点C按逆时针方向旋转得到△A′B′C,
∴AC=CA′=6,AB=B′A′=3,∠A=∠CA′B′,
∵CB′∥AB,
∴∠B′CA′=∠D,
∴△CAD∽△B′A′C,
∴$\frac{CA}{A′B′}=\frac{AD}{A′C}$,
∴$\frac{6}{3}=\frac{AD}{6}$,
解得AD=12,
∴BD=AD-AB=12-3=9.
故答案为:9.
点评 此题主要考查了旋转的性质以及相似三角形的判定与性质等知识,得出△CAD∽△B′A′C是解题关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
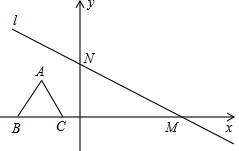 如图,在平面直角坐标系中,直线l:y=-$\frac{\sqrt{3}}{3}$x+4与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:
如图,在平面直角坐标系中,直线l:y=-$\frac{\sqrt{3}}{3}$x+4与x轴、y轴分别交于点M,N,高为3的等边三角形ABC,边BC在x轴上,将此三角形沿着x轴的正方向平移,在平移过程中,得到△A1B1C1,当点B1与原点重合时,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 评委代号 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ |
| 评分 | 85 | 90 | 80 | 95 | 90 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 两个同样的直角三角板如图所示摆放,使点F,B,E,C在一条直线上,则有DF∥AC,理由是内错角相等两直线平行
两个同样的直角三角板如图所示摆放,使点F,B,E,C在一条直线上,则有DF∥AC,理由是内错角相等两直线平行查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月用水量 | 不超过12t的部分 | 超过12t且不超过18t的部分 | 超过18t的部分 |
| 每吨收费标准(元) | 2 | 2.5 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com