【题目】如图，在
中，
，三条内角平分线交于点
，过点作
垂线，分别交
、
于点
、
，请写出图中相似的三角形，并说明其中两对相似的理由.
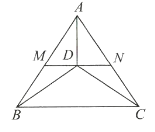
【答案】△ABD∽△ACD，△AMD∽△AND，△BMD∽△BDC∽△DNC，理由见解析
【解析】
根据角平分线和垂线的性质易证△AMD∽△AND，根据等腰三角形底角相等的性质可以判定∠ABD=∠ACD，即可证MN∥BC，进而可以证明△AMD∽△AND，△BMD∽△BDC∽△DNC，△ABD∽△ACD，即可解题．
解：△ABD∽△ACD，△AMD∽△AND，△BMD∽△BDC∽△DNC，
证明：△ABD∽△ACD，△AMD∽△AND，
∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABD=∠ACD，
∵AD为角平分线，
∴△ABD∽△ACD，
∵∠ADM=∠ADN，∠BAD=∠CAD，
∴△ADM∽△ADN．
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O直径，CD为⊙O的切线，C为切点，过A作CD的垂线，垂足为D．
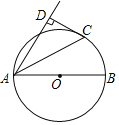
（1）求证：AC平分∠BAD；
（2）若⊙O半径为5，CD＝4，求AD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
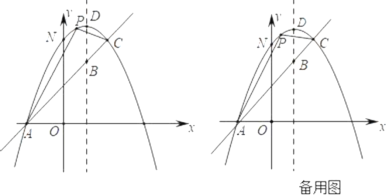
【题目】如图，已知抛物线y＝﹣x2+bx+c与一直线相交于A（﹣1，0），C（2，3）两点，与y轴交于点N，其顶点为D．
（1）求抛物线及直线AC的函数关系式；
（2）若P是抛物线上位于直线AC上方的一个动点，设点P的横坐标为t；
①当S△ACP＝S△ACN时，求点P的坐标；
②是否存在点P，使得△ACP是以AC为斜边的直角三角形？若存在，求点P的坐标；若不存在，请说明理由；
（3）若抛物线的对称轴与直线AC相交于点B，E为直线AC上的任意一点，过点E作EF∥BD交抛物线于点F，以B，D，E，F为顶点的四边形能否为平行四边形？若能，请直接写出点E的坐标；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
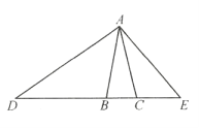
【题目】如图，已知等腰
中，
，点
在边
的反向延长线上，且
，点
在边的延长线上，且
，设
，
.
（1）求线段
的长；
（2）求
关于
的函数解析式，并写出定义域；
（3）当
平分
时，求线段
的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】投资1万元围一个矩形菜园(如图)，其中一边靠墙，另外三边选用不同材料建造.墙长24 m，平行于墙的边的费用为200元/m，垂直于墙的边的费用为150元/m，设平行于墙的边长为x m.
(1)设垂直于墙的一边长为y m，直接写出y与x之间的函数关系式；
(2)若菜园面积为384 m2，求x的值；
(3)求菜园的最大面积.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，
的顶点
在正方形
两条对角线的交点处，
，将绕点旋转，旋转过程中的两边分别与正方形的边
和
交于点
和点
（点与点
，
不重合）．
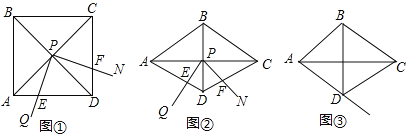
（1）如图①，当
时，求
，
，之间满足的数量关系，并证明；
（2）如图②，将图①中的正方形改为
的菱形，其他条件不变，当
时，（1）中的结论变为
，请给出证明；
（3）在（2）的条件下，若旋转过程中的边
与射线交于点，其他条件不变，探究在整个运动变化过程中，，，之间满足的数量关系，直接写出结论，不用加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y1=a（x+2）2-3与y2=
（x-3）2+1交于点A（1，3），过点A作x轴的平行线，分别交两条抛物线于点B，C．则以下结论：①无论x取何值，y2的值总是正数；②a=1；③当x=0时，y2-y1=4；④2AB=3AC；其中正确结论是（ ）
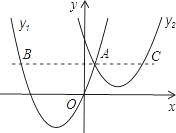
A.①②B.②③C.③④D.①④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，∠BAC＝90°，点F在BC边上，过A，B，F三点的⊙O交AC于另一点D，作直径AE，连结EF并延长交AC于点G，连结BE，BD，四边形BDGE是平行四边形．
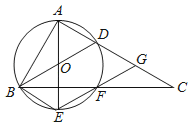
（1）求证：AB＝BF．
（2）当F为BC的中点，且AC＝3时，求⊙O的直径长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
