
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:初中数学 来源: 题型:
【题目】在一个木制的棱长为3的正方体的表面涂上颜色,将它的棱三等分,然后从等分点把正方体锯开,得到27个棱长为l的小正方体,将这些小正方体充分混合后,装入口袋,从这个口袋中任意取出一个小正方体,则这个小正方体的表面恰好涂有两面颜色的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AB=AC,∠B=∠C,BC=12厘米,点D为AB上一点且BD=8厘米,点P在线段BC上以2厘米/秒的速度由B点向C点运动,设运动时间为t,同时,点Q在线段CA上由C点向A点运动.
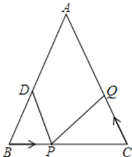
(1)用含t的式子表示PC的长为 ;
(2)若点Q的运动速度与点P的运动速度相等,当t=2时,△BPD与△CQP是否全等,请说明理由;
(3)若点Q的运动速度与点P的运动速度不相等,请求出点Q的运动速度是多少时,能够使△BPD与△CQP全等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上,点![]() 表示1,现将点
表示1,现将点![]() 沿
沿![]() 轴做如下移动,第一次点
轴做如下移动,第一次点![]() 向左移动3个单位长度到达点
向左移动3个单位长度到达点![]() ,第二次将点
,第二次将点![]() 向右移动6个单位长度到达点
向右移动6个单位长度到达点![]() ,第三次将点
,第三次将点![]() 向左移动9个单位长度到达点
向左移动9个单位长度到达点![]() ,按照这种移动规律移动下去,第
,按照这种移动规律移动下去,第![]() 次移动到点
次移动到点![]() ,如果点
,如果点![]() 与原点的距离不小于20,那么
与原点的距离不小于20,那么![]() 的最小值是__________.
的最小值是__________.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相交于 点E、F.若∠CBD=36°,则下列结论中不正确的是
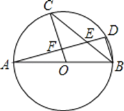
A. ∠AOC=72° B. ∠AEC=72° C. AF=DF D. BD=20F
查看答案和解析>>
科目:初中数学 来源: 题型:
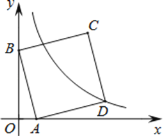
【题目】如图,在平面直角坐标系中,直线![]() 与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线
与x轴、y轴分别交于A、B两点,以AB为边在第一象限内作正方形ABCD,顶点D在双曲线![]() 上,将该正方形沿x轴负方向平移
上,将该正方形沿x轴负方向平移![]() 个单位长度后,顶点C恰好落在双曲线
个单位长度后,顶点C恰好落在双曲线![]() 上,则
上,则![]() 的值是_________.
的值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租车驾驶员从公司出发,在南北向的人民路上连续接送5批客人.行驶路程记录如下(规定向南为正,向北为负,单位:![]() ):
):
第1批 | 第2批 | 第3批 | 第4批 | 第5批 |
5 | 2 | -4 | -3 | 10 |
(1)接送完第5批客人后,该驾驶员在公司 边(填南或北),距离公司 千米.
(2)若该出租车每千米耗油0.2升,那么在这过程中共耗油 升.
(3)若该出租车的计价标准为:行驶路程不超过3![]() 收费10元,超过3
收费10元,超过3![]() 的部分按每千米1.8元收费,在这过程中该驾驶员共收到车费多少元?
的部分按每千米1.8元收费,在这过程中该驾驶员共收到车费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com