
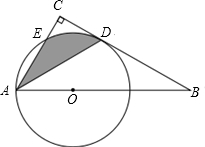
 如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.
如图,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与边BC交于点D,与边AC交于点E,连接AD,且AD平分∠BAC.分析 (1)连接OD,推出OD⊥BC,根据切线的判定推出即可;
(2)连接DE、OE,求出阴影部分的面积=扇形EOD的面积,求出扇形的面积即可.
解答 解:(1)BC与⊙O相切,
理由:连接OD,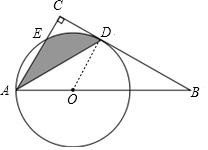
∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵AO=DO,
∴∠BAD=∠ADO,
∴∠CAD=∠ADO,
∴AC∥OD,
∵∠ACD=90°,
∴OD⊥BC,
∴BC与⊙O相切;
(2)连接OE,ED,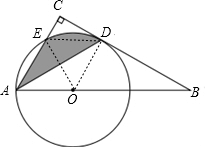
∵∠BAC=60°,OE=OA,
∴△OAE为等边三角形,
∴∠AOE=60°,
∴∠ADE=30°,
又∵∠OAD=$\frac{1}{2}$∠BAC=30°,
∴∠ADE=∠OAD,
∴ED∥AO,
∴S△AED=S△AOD,
∴阴影部分的面积=S扇形ODE=$\frac{60×π×4}{360}$=$\frac{2}{3}$π.
点评 本题考查了平行线的性质和判定,切线的性质和判定,扇形的面积有关计算的应用,能灵活运用定理进行推理和计算是解此题的关键.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,CE与BD相交于点M,BD与AC交于点N,试猜想BD与CE有何关系?说明理由.
如图所示,在Rt△ABC和Rt△ADE中,AB=AC,AD=AE,CE与BD相交于点M,BD与AC交于点N,试猜想BD与CE有何关系?说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
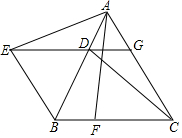 如图,△ABC是等边三角形,过AB边上的点D作GD∥BC,交AC于点G,在GD的延长线上取点E,使DE=DB,连接AE、CD;
如图,△ABC是等边三角形,过AB边上的点D作GD∥BC,交AC于点G,在GD的延长线上取点E,使DE=DB,连接AE、CD;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每日涨跌 | +4 | +4.5 | -1 | -2.5 | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,正方形网格中的每个小正方形的边长都是1,每个顶点叫做格点,在图中以格点为顶点画一个三角形,使它的三边长都是整数(作图痕迹用黑色签字笔加粗加黑)
如图,正方形网格中的每个小正方形的边长都是1,每个顶点叫做格点,在图中以格点为顶点画一个三角形,使它的三边长都是整数(作图痕迹用黑色签字笔加粗加黑)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com