
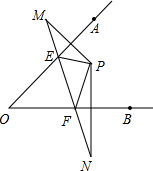
 如图,点P在∠AOB内,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于E、F,若∠EPF=α,则∠AOB=90°-$\frac{1}{2}$α.
如图,点P在∠AOB内,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于E、F,若∠EPF=α,则∠AOB=90°-$\frac{1}{2}$α. 分析 连接OP、OM、ON,根据轴对称的性质可得OP=PM=ON,∠OPE=∠OME,∠OPF=∠ONF,∠POE=∠MOE,∠POF=∠NOF,然后求出∠OME+∠ONF=∠EPF=α,再根据三角形的内角和等于180°求出∠MON,然后求解即可.
解答 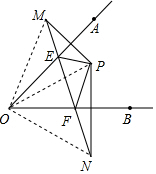 解:如图,连接OP、OM、ON,
解:如图,连接OP、OM、ON,
∵点M、N分别是点P关于直线OA、OB的对称点,
∴OP=PM=ON,∠OPE=∠OME,∠OPF=∠ONF,∠POE=∠MOE,∠POF=∠NOF,
∴∠OME+∠ONF=∠OPE+∠OPF=∠EPF=α,
在△OMN中,∠MON=180°-(∠OME+∠ONF)=180°-α,
∵∠MON=∠MOE+∠POE+∠POF+∠NOF=2(∠POE+∠POF)=2∠AOB,
∴∠AOB=$\frac{1}{2}$∠MON=$\frac{1}{2}$(180°-α)=90°-$\frac{1}{2}$α.
故答案为:90°-$\frac{1}{2}$α.
点评 本题考查了轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
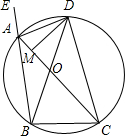 如图,△ABC内接于⊙O,其外角平分线AD交⊙O于D,DM⊥AC于M,下列结论中正确的是①②③.
如图,△ABC内接于⊙O,其外角平分线AD交⊙O于D,DM⊥AC于M,下列结论中正确的是①②③.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com