
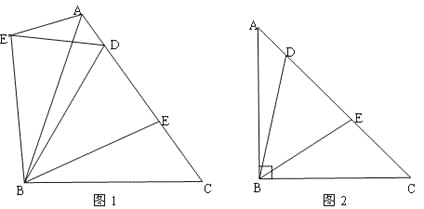
【题目】(1)如图1,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=![]() ∠ABC(0°<∠CBE<
∠ABC(0°<∠CBE<![]() ∠ABC).以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE′A(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;
∠ABC).以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC,得到△BE′A(点C与点A重合,点E到点E′处),连接DE′.求证:DE′=DE;
(2)如图2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC边上的两点,
且满足∠DBE=![]() ∠ABC(0°<∠CBE<45°) .求证:DE2=AD2+EC2.
∠ABC(0°<∠CBE<45°) .求证:DE2=AD2+EC2.
【答案】(1)证明见解析;(2)证明见解析
【解析】
(1)由旋转的性质易得BE′=BE,∠E’BA=∠EBC,由已知∠DBE=![]() ∠ABC经等量代换可得∠E′BD=∠DBE,从而可由SAS得△E’BD≌△EBD,得到DE′=DE;
∠ABC经等量代换可得∠E′BD=∠DBE,从而可由SAS得△E’BD≌△EBD,得到DE′=DE;
(2)由(1)的启示,作如(1)的辅助图形,即可得到直角三角形DE′A,根据勾股定理即可证得结论.
解:(1)∵△BE′A是△BEC按逆时针方向旋转∠ABC得到,
∴BE′=BE,∠E′BA=∠EBC.
∵∠DBE=![]() ∠ABC,∴∠ABD+∠EBC =
∠ABC,∴∠ABD+∠EBC =![]() ∠ABC.
∠ABC.
∴∠ABD+∠E′BA =![]() ∠ABC,即∠E′BD=
∠ABC,即∠E′BD=![]() ∠ABC.∴∠E′BD=∠DBE.
∠ABC.∴∠E′BD=∠DBE.
在△E′BD和△EBD中,∵BE′=BE,∠E’BD=∠DBE,BD=BD,
∴△E′BD≌△EBD(SAS).
∴DE′=DE.
(2)以点B为旋转中心,将△BEC按逆时针方向旋转∠ABC=90°,得到△BE′A(点C与点A重合,点E到点E′处),连接DE′.
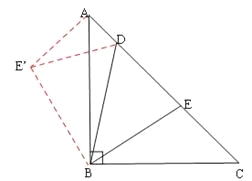
由(1)知DE′=DE.
由旋转的性质,知E′A=EC,∠E′ AB=∠ECB.
又∵BA=BC,∠ABC=90°,∴∠BAC=∠ACB=45°.
∴∠E′AD=∠E′AB+∠BAC=90°.
在Rt△DE′A中,DE′2=AD2+E′A2,
∴DE2=AD2+EC2.


科目:初中数学 来源: 题型:
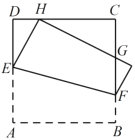
【题目】如图,将正方形![]() 折叠,使顶点
折叠,使顶点![]() 与
与![]() 边上的一点
边上的一点![]() 重合(
重合(![]() 不与端点
不与端点![]() ,
,![]() 重合),折痕交
重合),折痕交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,边
,边![]() 折叠后与边
折叠后与边![]() 交于点
交于点![]() ,设正方形
,设正方形![]() 的周长为
的周长为![]() ,
,![]() 的周长为
的周长为![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年3月24日,工信部发布《关于推动![]() 加快发展的通知》,全力推进
加快发展的通知》,全力推进![]() 网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向
网络建设、应用推广、技术发展和安全保障.工信部提出,要培育新型消费模式,加快用户向![]() 迁移,推动“
迁移,推动“![]() 医疗健康”创新发展,实施“
医疗健康”创新发展,实施“![]() 工业互联网”512工程,促进“
工业互联网”512工程,促进“![]() 车联网”协同发展,构建
车联网”协同发展,构建![]() 应用生态系统.现“
应用生态系统.现“![]() 网络”已成为一个热门词汇,某校为了解九年级学生对“
网络”已成为一个热门词汇,某校为了解九年级学生对“![]() 网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
网络”的了解程度,对九年级学生行了一次测试(一共10道题答对1道得1分,满分10分),测试结束后随机抽取了部分学生的成绩整理分析,绘制出如图所示的两幅不完整的统计图,请根据图中信息解答下列问题:
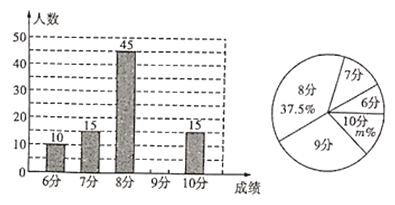
(1)请补全条形统计图,扇形统计图中![]() __;
__;
(2)所调查学生成绩的众数是_ ____分,平均数是_ 分;
(3)若该校九年级学生有![]() 人,请估计得分不少于
人,请估计得分不少于![]() 分的有多少人?
分的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
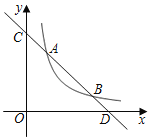
【题目】如图,已知一次函数y1=kx+b与反比例函数y2=![]() (x>0)的图象分别交于点A(2,4)和点B(4,n),与坐标轴分别交于点C和点D.
(x>0)的图象分别交于点A(2,4)和点B(4,n),与坐标轴分别交于点C和点D.
(1)求反比例函数和一次函数的解析式;
(2)求y1<y2时,自变量x的取值范围;
(3)若点P是x轴上一动点,当△ABP为直角三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
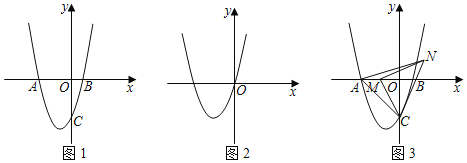
【题目】已知在平面直角坐标系中,抛物线y=x2+3x﹣a2+a+2(a>1)的图象交x轴于点A和点B(点A在点B左侧),与y轴交于点C,顶点为E.
(1)如图1,求线段AB的长度(用含a的式子表示)及抛物线的对称轴;
(2)如图2,当抛物线的图象经过原点时,在平面内是否存在一点P,使得以A、B、E、P为顶点的四边形能否成为平行四边形?如果能,求出P点坐标;如果不能,请说明理由;
(3)如图3,当a=3时,若M点为x轴上一动点,连结MC,将线段MC绕点M逆时针旋转90°得到线段MN,连结AC、CN、AN,则△ACN周长的最小值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
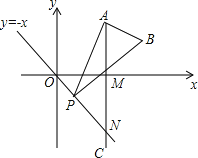
【题目】如图,已知点A是第一象限内横坐标为![]() 的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是_____.
的一个定点,AC⊥x轴于点M,交直线y=﹣x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
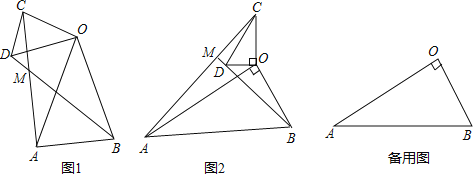
如图1,在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=40°,连接AC,BD交于点M.填空:
①![]() 的值为 ;
的值为 ;
②∠AMB的度数为 .
(2)类比探究
如图2,在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC交BD的延长线于点M.请判断![]() 的值及∠AMB的度数,并说明理由;
的值及∠AMB的度数,并说明理由;
(3)拓展延伸
在(2)的条件下,将△OCD绕点O在平面内旋转,AC,BD所在直线交于点M,若OD=1,OB=![]() ,请直接写出当点C与点M重合时AC的长.
,请直接写出当点C与点M重合时AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
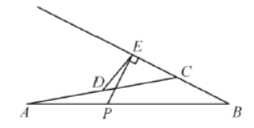
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 是边
是边![]() 上的一个动点,过点
上的一个动点,过点![]() 作射线
作射线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,连接
,连接![]() .设
.设![]() ,
,![]() .小石根据学习函数的经验,对函数
.小石根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
的变化而变化的规律进行了探究.下面是小石的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如表:
的几组值,如表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(说明:补全表格时相关数据保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:点![]() 是
是![]() 边的中点时,
边的中点时,![]() 的长度约为_______
的长度约为_______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早上匀速骑车去上学,出发几分钟后,爸爸发现小明的作业本丢在家里,赶紧匀速骑车去追.爸爸刚出发![]() 时,小明也发现作业本丢在家里,立刻按原路原速返回,
时,小明也发现作业本丢在家里,立刻按原路原速返回, ![]() 后遇到爸爸,爸爸把作业本交给小明后立刻按原路原速返回家,小明继续按原速骑车赶往学校.小明和爸爸相距的路程
后遇到爸爸,爸爸把作业本交给小明后立刻按原路原速返回家,小明继续按原速骑车赶往学校.小明和爸爸相距的路程![]() 与小明出发的时间
与小明出发的时间![]() 之间的关系如图所示(爸爸给小明作业本的时间忽略不计).下列说法中,错误的是( )
之间的关系如图所示(爸爸给小明作业本的时间忽略不计).下列说法中,错误的是( )
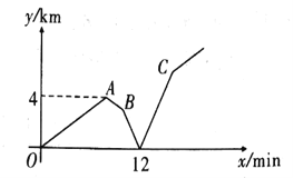
A.小明的骑车速度为![]() B.爸爸骑车的速度是小明的
B.爸爸骑车的速度是小明的![]() 倍
倍
C.点![]() 坐标为
坐标为![]() D.爸爸返回家时,小明共骑行了
D.爸爸返回家时,小明共骑行了![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com