
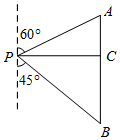
 如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(60+20$\sqrt{3}$)米.
如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离(60+20$\sqrt{3}$)米. 分析 由已知可得△ABP中∠A=60°∠B=45°且PC=60m,要求AB的长,可以先求出AC和BC的长就可转化为运用三角函数解直角三角形.
解答  解:由题意可知:
解:由题意可知:
∠ACP=∠BCP=90°,∠APC=30°,∠BPC=45°.
在Rt△BPC中,
∵∠BCP=90°,∠B=∠BPC=45°,
∴BC=PC=60.
在Rt△ACP中,
∵∠ACP=90°,∠APC=30°,
tan30°=$\frac{AC}{PC}$,
∴AC=PC•tan30°=tan30°×60=60×$\frac{\sqrt{3}}{3}$=20$\sqrt{3}$(米).
∴AB=AC+BC=60+20$\sqrt{3}$(米).
答:教学楼A与办公楼B之间的距离是(60+20$\sqrt{3}$)米.
故答案是:(60+20$\sqrt{3}$)米.
点评 本题考查了解直角三角形的应用--方向角问题.解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:解答题
 如图,已知∠ABC=31°,∠1=∠2,求∠A的度数.
如图,已知∠ABC=31°,∠1=∠2,求∠A的度数.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大3倍 | C. | 缩小3倍 | D. | 扩大9倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
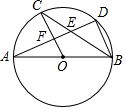 如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②CB平分∠ABD;③∠AOC=∠AEC;④AF=DF;⑤△CEF≌△BED;⑥BD=2OF.其中一定成立的是(请填序号)①②④⑥.
如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:①AD⊥BD;②CB平分∠ABD;③∠AOC=∠AEC;④AF=DF;⑤△CEF≌△BED;⑥BD=2OF.其中一定成立的是(请填序号)①②④⑥.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com