
ЁОЬтФПЁПШчЭМЂйЃЌдкОиаЮABCDжаЃЌAB=![]() ЃЌAD=3ЃЌЕуEЪЧБпADППНќAЕФШ§ЕШЗжЕуЃЌЕуPЪЧBCбгГЄЯпЩЯвЛЕуЃЌЧвEPЁЭEBЃЌЕуGЪЧBEЩЯШЮвтвЛЕуЃЌЙ§GзїGHЁЮBPЃЌНЛEPгкЕуHЃЎНЋЁїEGHШЦЕуEФцЪБеыа§зЊІСЃЈ0ЃМІСЃМ90ЁуЃЉЃЌЕУЕНЁїEMNЃЈMЁЂNЗжБ№ЪЧGЁЂHЕФЖдгІЕуЃЉЃЎ
ЃЌAD=3ЃЌЕуEЪЧБпADППНќAЕФШ§ЕШЗжЕуЃЌЕуPЪЧBCбгГЄЯпЩЯвЛЕуЃЌЧвEPЁЭEBЃЌЕуGЪЧBEЩЯШЮвтвЛЕуЃЌЙ§GзїGHЁЮBPЃЌНЛEPгкЕуHЃЎНЋЁїEGHШЦЕуEФцЪБеыа§зЊІСЃЈ0ЃМІСЃМ90ЁуЃЉЃЌЕУЕНЁїEMNЃЈMЁЂNЗжБ№ЪЧGЁЂHЕФЖдгІЕуЃЉЃЎ
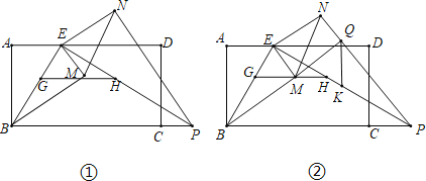
ЃЈ1ЃЉЧѓBPЕФГЄЃЛ
ЃЈ2ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШчЭМЂкЕБІС=60ЁуЪБЃЌЕуMЧЁКУТфдкGHЩЯЃЌбгГЄBMНЛNPгкЕуQЃЌШЁEPЕФжаЕуKЃЌСЌНгQKЃЎШєЕуGдкЯпЖЮEBЩЯдЫЖЏЃЌЮЪQKЪЧЗёгазюаЁжЕЃПШєгазюаЁжЕЃЌЧыЧѓГіЕуGдЫЖЏЕНEBЕФЪВУДЮЛжУЪБЃЌQKгазюаЁжЕМАзюаЁжЕЪЧЖрЩйЃЌШєУЛгазюаЁжЕЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉPB=4ЃЛЃЈ2ЃЉ![]() =
=![]() ЃЛЃЈ3ЃЉЕуGдЫЖЏЕНEBЕФжаЕуЮЛжУЪБЃЌQKгазюаЁжЕЃЌзюаЁжЕЮЊ1ЃЎ
ЃЛЃЈ3ЃЉЕуGдЫЖЏЕНEBЕФжаЕуЮЛжУЪБЃЌQKгазюаЁжЕЃЌзюаЁжЕЮЊ1ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЙДЙЩЖЈРэЕУBE=2ЃЌвзжЄЁїBAEЁзЁїPEBЃЌДгЖјЕУ![]() =
=![]() ЃЌМДПЩЧѓНтЃЛ
ЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉгЩtanЁЯABE=![]() =
=![]() ЃЌПЩЕУЁЯABE=30ЁуЃЌНсКЯа§зЊЕФаджЪЕУPE=
ЃЌПЩЕУЁЯABE=30ЁуЃЌНсКЯа§зЊЕФаджЪЕУPE=![]() EBЃЌEN=
EBЃЌEN=![]() EMЃЌЁЯBEM=ЁЯPENЃЌНјЖјЕУГіЁїBEMЁзЁїPENЃЌМДПЩЧѓНтЃЛ
EMЃЌЁЯBEM=ЁЯPENЃЌНјЖјЕУГіЁїBEMЁзЁїPENЃЌМДПЩЧѓНтЃЛ
ЃЈ3ЃЉШЁPBЕФжаЕуOЃЌСЌНгOQЃЌOKЃЎЩшBQНЛPEгкJЃЌвзЕУBEJ=ЁЯPQJ=90ЁуЃЌДгЖјЕУЕНOQ =2ЃЌOK=1ЃЌгЩQKЁнOQ-OKЃЌПЩЕУQKЕФзюаЁжЕЮЊ1ЃЌДЫЪБOЃЌKЃЌQЙВЯпЃЌШЛКѓИљОнІС=60ЁужЄУїEGMЪЧЕШБпШ§НЧаЮЃЌЧѓГіЁЯEBM=30ЁуЃЌЁЯGMB=30ЁуМДПЩЕУНтЃЎ
ЃЈ1ЃЉШчЭМЂйжаЃЌ
ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯA=ЁЯABC=90ЁуЃЌ
ЁпAE=![]() AD=1ЃЌAB=
AD=1ЃЌAB=![]() ЃЌ
ЃЌ
ЁрBE=![]() =2ЃЌ
=2ЃЌ
ЁпBEЁЭPEЃЌ
ЁрЁЯPEB=90ЁуЃЌ
ЁрЁЯABE+ЁЯCBE=90ЁуЃЌЁЯCBE+ЁЯEPB=90ЁуЃЌ
ЁрЁЯABE=ЁЯEPBЃЌ
ЁпЁЯA=ЁЯBEP=90ЁуЃЌ
ЁрЁїBAEЁзЁїPEBЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
ЁрPB=![]() =4ЃЛ
=4ЃЛ
ЃЈ2ЃЉЁпдкRtЁїABEжаЃЌ tanЁЯABE=![]() =
=![]() ЃЌ
ЃЌ
ЁрЁЯABE=30ЁуЃЌ
ЁпЁЯABC=90ЁуЃЌ
ЁрЁЯEBC=60ЁуЃЌ
ЁпGHЁЮBCЃЌ
ЁрЁЯEGH=ЁЯEBC=ЁЯEMN=60ЁуЃЌ
ЁпЁЯMEN=ЁЯGEH=90ЁуЃЌ
ЁрPE=![]() EBЃЌEN=
EBЃЌEN=![]() EMЃЌ
EMЃЌ
Ёр![]() =
=![]() =
=![]() ЃЌ
ЃЌ
ЁпЁЯPEB=ЁЯMEN=90ЁуЃЌ
ЁрЁЯBEM=ЁЯPENЃЌ
ЁрЁїBEMЁзЁїPENЃЌ
Ёр![]() =
=![]() =
=![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ2жаЃЌШЁPBЕФжаЕуOЃЌСЌНгOQЃЌOKЃЎЩшBQНЛPEгкJЃЎ
ЁпЁїBEMЁзЁїPENЃЌ
ЁрЁЯEBM=ЁЯEPNЃЌ
ЁпЁЯBJE=ЁЯPJQЃЌ
ЁрЁЯBEJ=ЁЯPQJ=90ЁуЃЌ
ЁпBO=OPЃЌ
ЁрOQ=![]() PB=2ЃЌ
PB=2ЃЌ
ЁпPO=OBЃЌPK=KEЃЌ
ЁрOK=![]() BE=1ЃЌ
BE=1ЃЌ
ЁрQKЁнOQ-OK=1ЃЌ
ЁрQKЕФзюаЁжЕЮЊ1ЃЌДЫЪБOЃЌKЃЌQЙВЯпЃЌ
ЁрOQЁЮBEЃЌ
ЁрЁЯQOP=ЁЯEBP=60ЁуЃЌ
ЁпІС=60ЁуЪБЃЌЕуMЧЁКУТфдкGHЩЯЃЌ
ЁрЁЯEGM=60ЁуЃЌ
ЁрEGMЪЧЕШБпШ§НЧаЮЃЌ
гжЁпOQ=OBЃЌ
ЁрЁЯOBQ=![]() ЁС60Ёу=30ЁуЃЌ
ЁС60Ёу=30ЁуЃЌ
ЁрЁЯEBM=ЁЯEBP-ЁЯOBQ=60Ёу-30Ёу=30ЁуЃЌ
ЁрЁЯGMB=ЁЯEGM-ЁЯEBM=60Ёу-30Ёу=30ЁуЃЌ
ЁрBG=GM=GEЃЌ
ЁрЕуGЪЧBEЕФжаЕуЃЌ
злЩЯЫљЪіЃКЕуGдЫЖЏЕНEBЕФжаЕуЮЛжУЪБЃЌQKгазюаЁжЕЃЌзюаЁжЕЮЊ1ЃЎ




| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
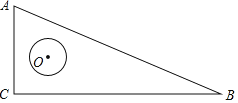
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌACЃКBCЃКABЃН5ЃК12ЃК13ЃЌЁбOдкЁїABCФкздгЩвЦЖЏЃЌШєЁбOЕФАыОЖЮЊ1ЃЌЧвдВаФOдкЁїABCФкЫљФмЕНДяЕФЧјгђЕФУцЛ§ЮЊ![]() ЃЌдђЁїABCЕФжмГЄЮЊ_____ЃЎ
ЃЌдђЁїABCЕФжмГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТБэЃК
x | 0 | 1 | 2 |
ax2 | ЁЁ ЁЁ | 1 | ЁЁ ЁЁ |
ax2+bx+c | Љ3 | ЁЁ ЁЁ | Љ3 |
ЃЈ1ЃЉЧѓaЁЂbЁЂcЕФжЕЃЌВЂдкБэФкПеИёДІЬюШые§ШЗЕФЪ§ЃЛ
ЃЈ2ЃЉИљОнЩЯУцЕФНсЙћНтД№ЮЪЬтЃК
ЂйдкЗНИёжНжаЛГіКЏЪ§yЃНax2+bx+cЕФЭМЯѓЃЛ
ЂкИљОнЭМЯѓЛиД№ЃКЕБxЕФШЁжЕЗЖЮЇЪЧЁЁ ЁЁЪБЃЌyЁм0ЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ЖЈвхЃКдкЭЙЫФБпаЮжаЃЌЮвУЧАбСНзщЖдБпГЫЛ§ЕФКЭЕШгкЖдНЧЯпЕФГЫЛ§ЕФЫФБпаЮГЦЮЊЁАЭъУРЫФБпаЮЁБ
ЃЈ1ЃЉдке§ЗНаЮЁЂОиаЮЁЂСтаЮжаЃЌвЛЖЈЪЧЁАЭъУРЫФБпаЮЁБЕФЪЧ______ЃЎ
ЃЈ2ЃЉШчЭМ1ЃЌдкЁїABCжаЃЌAB=2ЃЌBC=![]() ЃЌAC=3ЃЌDЮЊЦНУцФквЛЕуЃЌвдAЁЂBЁЂCЁЂDЫФЕуЮЊЖЅЕуЙЙГЩЕФЫФБпаЮЮЊЁАЭъУРЫФБпаЮЁБЃЌШєDAЃЌDCЕФГЄЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬx2-(m+3)x+
ЃЌAC=3ЃЌDЮЊЦНУцФквЛЕуЃЌвдAЁЂBЁЂCЁЂDЫФЕуЮЊЖЅЕуЙЙГЩЕФЫФБпаЮЮЊЁАЭъУРЫФБпаЮЁБЃЌШєDAЃЌDCЕФГЄЪЧЙигкxЕФвЛдЊЖўДЮЗНГЬx2-(m+3)x+![]() (5m2-2m+13)=0(ЦфжаmЮЊГЃЪ§)ЕФСНИіИљЃЌЧѓЯпЖЮBDЕФГЄЖШЃЎ
(5m2-2m+13)=0(ЦфжаmЮЊГЃЪ§)ЕФСНИіИљЃЌЧѓЯпЖЮBDЕФГЄЖШЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌдкЁАЭъУРЫФБпаЮЁБEFGHжаЃЌЁЯF=90ЁуЃЌEF=6ЃЌFG=8ЃЌЧѓЁАЭъУРЫФБпаЮЁБEFGHУцЛ§ЕФзюДѓжЕЃЎ
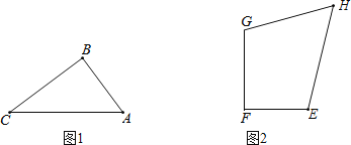
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтФГаЃЦпФъМЖбЇЩњзївЕЪБМфЧщПіЃЌЫцЛњГщШЁСЫИУаЃЦпФъМЖВПЗжбЇЩњНјааЕїВщЃЌВЂИљОнЕїВщНсЙћЛцжЦСЫШчЯТЕФЭГМЦЭМЃЎ
зївЕЪБМфЗжзщБэЃЈЕЅЮЛЃКаЁЪБЃЉ
Б№ | зївЕЪБМф | ШЫЪ§ | ЦЕТЪ |
A | 1ЁмxЁм1.5 | 5 | 0.1 |
B | 1.5ЁмxЁм2 | 20 | b |
C | 2ЁмxЁм2.5 | m | n |
D | xЁн2.5 | 7 | 0.14 |
аЁМЦ | a | 1 |
ЃЈ1ЃЉЭГМЦЭМжаЕФa=______ЃЛb=______ЃЛm=______ЃЛn=______ЃЎ
ЃЈ2ЃЉЧѓГіCзщЕФЩШаЮЕФдВаФНЧЖШЪ§ЃЎ
ЃЈ3ЃЉШчЙћИУаЃЦпФъМЖбЇЩњЙВ400УћЃЌЪдЙРМЦет400УћЩњзївЕЪБМфдкBзщКЭCзщЕФШЫЪ§ЙВгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
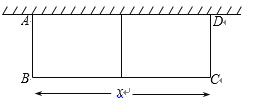
ЁОЬтФПЁПШчЭМЃЌРћгУвЛУцЧНЃЈЧНЕФГЄЖШЮЊ15 mЃЉЃЌгУРщАЪЮЇГЩвЛИіОиаЮЛЈдАABCDЃЌжаМфдйгУвЛЕРРщАЪИєГЩСНИіаЁОиаЮЃЌЙВгУШЅРщАЪ42 m.ЩшЦНаагкЧНЕФвЛБпBCГЄЮЊx mЃЌЛЈдАЕФУцЛ§ЮЊS m2ЃЎ
ЃЈ1ЃЉЧѓSгыxжЎМфЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЮЪЛЈдАУцЛ§ПЩвдДяЕН120ЦНЗНУзТ№ЃПШчЙћФмЃЌЛЈдАЕФГЄКЭПэИїЪЧЖрЩйЃПШчЙћВЛФмЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
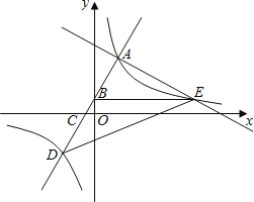
ЁОЬтФПЁПШчЭМЃЌжБЯпy=2x+bгыЫЋЧњЯпy=![]() ЃЈkЃО0ЃЉНЛгкЕуAЁЂDЃЌжБЯпADНЛyжсЁЂxжсгкЕуBЁЂCЃЌжБЯпy=-
ЃЈkЃО0ЃЉНЛгкЕуAЁЂDЃЌжБЯпADНЛyжсЁЂxжсгкЕуBЁЂCЃЌжБЯпy=-![]() +nЙ§ЕуAЃЌгыЫЋЧњЯпy=
+nЙ§ЕуAЃЌгыЫЋЧњЯпy=![]() ЃЈkЃО0ЃЉЕФСэвЛИіНЛЕуЮЊЕуEЃЌСЌНгBEЁЂDEЃЌШєSЁїABE=4ЃЌЧвSЁїABEЃКSЁїDBE=3ЃК4ЃЌдђkЕФжЕЮЊ___ЃЎ
ЃЈkЃО0ЃЉЕФСэвЛИіНЛЕуЮЊЕуEЃЌСЌНгBEЁЂDEЃЌШєSЁїABE=4ЃЌЧвSЁїABEЃКSЁїDBE=3ЃК4ЃЌдђkЕФжЕЮЊ___ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгавЛ СаЪ§ЪЧ7ЁЂ9ЁЂ3ЁЂ7ЁЂ6ЁЂ9ЁЂ11ЁЂ8ЁЂ 2ЁЂ9ЁЂ10ЃЌжаЮЛЪ§ЪЧЖрЩйЃПетСаЪ§ШєдйМгШы3КЭ1000СНИіЪ§ЃЌФЧУДжаЮЛЪ§ЛсИФБфТ№ЃПЦНОљЪ§гжЛсгаЪВУДБфЛЏЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
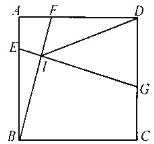
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ6ЕФе§ЗНаЮABCDжаЃЌЕуEЁЂFЁЂGЗжБ№дкБпABЁЂADЁЂCDЩЯЃЌEGгыBFНЛгкЕуIЃЌAE=2ЃЌBF=EGЃЌDG>AEЃЌдђDIЕФзюаЁжЕЮЊ________.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com