
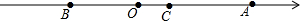 如图,在数轴上原点O表示的数是0,B点表示的数是m,A表示的数是n,且(m+4)2+|n-8|=0.
如图,在数轴上原点O表示的数是0,B点表示的数是m,A表示的数是n,且(m+4)2+|n-8|=0.分析 (1)根据非负数的性质求得m、n的值,即点B、A分别表示的实数,然后根据线段中点的求法和两实数间的距离的求法进行解答;
(2)设点P的运动速度是x,则点Q的运动速度是3x,根据t=13时,线段PQ的长为14个单位长度列出关于x的方程并解答;
(3)先表示出t秒后点P、Q、N所表示的数,继而表示出PQ、NQ的长,根据PQ=2NQ列出关于t的绝对值方程,解方程可得t的值.
解答 解:(1)由(m+4)2+|n-8|=0得到:m=-4,n=8,
则B点表示的数是-4,A表示的数是8,
所以点C表示的数是:$\frac{8-4}{2}$=2,
则CO=2;
(2)设点P的运动速度是x,则点Q的运动速度是3x,
依题意得:|13×3x-13x-12|=14,
解得x=1或x=-$\frac{1}{13}$(舍),
所以3x=3.
答:点P的运动速度是1,则点Q的运动速度是3.
(3)根据题意知点Q表示的数为-$\frac{4}{3}$t,点P表示的数为-4-t,点Q表示的数为8-3t,
则PQ=|8-3t-(-4-t)|=|12-2t|,NQ=|8-3t-(-$\frac{4}{3}$t)|=|8-$\frac{5}{3}$t|,
∵PQ=2NQ,
∴|12-2t|=2|8-$\frac{5}{3}$t|,
则12-2t=16-$\frac{10}{3}$t或12-2t=$\frac{10}{3}$t-16,
解得:t=3或t=$\frac{21}{4}$,
当t=3时,点N表示的数为-4,
当t=$\frac{21}{4}$时,点N表示的数为-7.
点评 本题主要考查数轴、非负数的性质及一元一次方程的应用,根据两点间的距离公式表示出所需线段的长度是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=6cm,直线CM⊥BC,动点D从点C开始以每秒2cm的速度运动到B点,动点E也同时从点C开始沿射线CM方向以每秒1cm的速度运动.
如图,在△ABC中,已知AB=AC,∠BAC=90°,BC=6cm,直线CM⊥BC,动点D从点C开始以每秒2cm的速度运动到B点,动点E也同时从点C开始沿射线CM方向以每秒1cm的速度运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 向东走100m | B. | 向西走100m | C. | 向西走-100m | D. | 向西走10m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
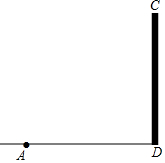 小明同学去大埋旅游时看见一座占塔,他在父母帮助下测得一些数据,首先在地面上的A点测得塔C的仰角为30°,然后沿着向塔的方向前进10m到达B点(点B在线段AD上),则B点测得塔顶C的仰角为45°,请你在图中补画示意图,并求出塔高(精确到0.1m)
小明同学去大埋旅游时看见一座占塔,他在父母帮助下测得一些数据,首先在地面上的A点测得塔C的仰角为30°,然后沿着向塔的方向前进10m到达B点(点B在线段AD上),则B点测得塔顶C的仰角为45°,请你在图中补画示意图,并求出塔高(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 二次函数y=ax2+bx+c(a≠0)的图象如图,请结合图象,解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图,请结合图象,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.
如图,直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边△AOB,点C为x正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,直线DA交y轴于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | sinA=$\frac{AC}{AB}$ | B. | cosA=$\frac{AD}{AC}$ | C. | tanA=$\frac{CD}{BD}$ | D. | cotA=$\frac{CD}{AD}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com