
 如图,小方格是边长为1的正方形,则四边形ABCD的周长为15+3$\sqrt{5}$+$\sqrt{26}$.
如图,小方格是边长为1的正方形,则四边形ABCD的周长为15+3$\sqrt{5}$+$\sqrt{26}$. 分析 根据勾股定理求出四边形ABCD的边长,根据周长公式计算即可.
解答 解:由勾股定理得,AD=$\sqrt{{3}^{2}+{4}^{2}}$=5,
AB=$\sqrt{{5}^{2}+{1}^{2}}$=$\sqrt{26}$,
BC=$\sqrt{{8}^{2}+{6}^{2}}$=10,
CD=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∴四边形ABCD的周长=AD+CD+BC+AB=15+3$\sqrt{5}$+$\sqrt{26}$,
故答案为:15+3$\sqrt{5}$+$\sqrt{26}$.
点评 本题考查的是勾股定理的应用,在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.如果直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.


科目:初中数学 来源: 题型:填空题
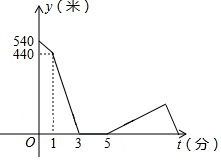 “欢乐跑中国•重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了$\frac{49}{3}$分钟.
“欢乐跑中国•重庆站”比赛前夕,小刚和小强相约晨练跑步.小刚比小强早1分钟跑步出门,3分钟后他们相遇.两人寒暄2分钟后,决定进行跑步比赛.比赛时小刚的速度始终是180米/分,小强的速度是220米/分.比赛开始10分钟后,因雾霾严重,小强突感身体不适,于是他按原路以出门时的速度返回,直到他们再次相遇.如图所示是小刚、小强之间的距离y(千米)与小刚跑步所用时间x(分钟)之间的函数图象.问小刚从家出发到他们再次相遇时,一共用了$\frac{49}{3}$分钟.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知实数a、b在数轴上的位置如图所示,试化简:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$.
已知实数a、b在数轴上的位置如图所示,试化简:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com