
 如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP=8.
如图,在△ABC中,BC=4,E、F分别是AB、AC上的点,且EF∥BC,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于Q,当3CQ=CE时,EP+BP=8. 分析 如图,延长EF交BQ的延长线于G.首先证明PB=PG,EP+PB=EG,由EG∥BC,推出$\frac{EG}{BC}$=$\frac{EQ}{QC}$=2,即可求出EG解决问题.
解答 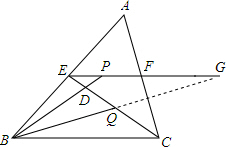 解:如图,延长EF交BQ的延长线于G.
解:如图,延长EF交BQ的延长线于G.
∵EG∥BC,
∴∠G=∠GBC,
∵∠GBC=∠GBP,
∴∠G=∠PBG,
∴PB=PG,
∴PE+PB=PE+PG=EG,
∵3CQ=EC,
∴EQ=2CQ,
∵EG∥BC,
∴$\frac{EG}{BC}$=$\frac{EQ}{QC}$=2,∵BC=4,
∴EG=8,
∴EP+PB=EG=8,
故答案为:8.
点评 本题考查平行线分线段成比例定理、角平分线的定义、等腰三角形的判定和性质等知识,解题的关键是学会添加辅助线构造等腰三角形解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.
如图,等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,使AE=CF,连接AF,BE相交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
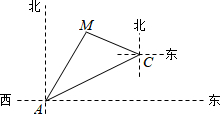 如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西75°方向,请你在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,并求出管道MN的长度(精确到0.1米).
如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市北偏东30°方向,测绘员沿主输气管道步行2000米到达C处,测得小区M位于C的北偏西75°方向,请你在主输气管道上寻找支管道连接点N,使到该小区铺设的管道最短,并求出管道MN的长度(精确到0.1米).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
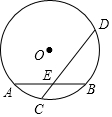 如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )
如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )| A. | 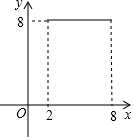 | B. |  | C. | 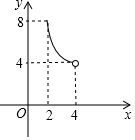 | D. | 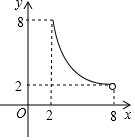 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com