
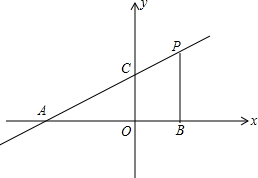
 若直线y=
若直线y= x+2分别交x轴、y轴于A、C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6.
x+2分别交x轴、y轴于A、C两点,点P是该直线上在第一象限内的一点,PB⊥x轴,B为垂足,且S△ABC=6. x+2=0,解得x=-4,
x+2=0,解得x=-4, a+2),且a>0,
a+2),且a>0,
 (a+4)×2=6,
(a+4)×2=6, x-1,
x-1, a+2),即可得到点B的坐标(a,0),然后根据△ABC的面积列式求出a的值,从而得解;
a+2),即可得到点B的坐标(a,0),然后根据△ABC的面积列式求出a的值,从而得解;

科目:初中数学 来源: 题型:
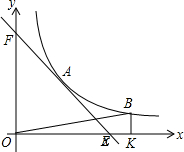 已知A(m,2)是直线L和双曲线y=
已知A(m,2)是直线L和双曲线y=| 3 |
| x |
| 3 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
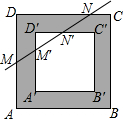 我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,已知方形环四周的宽度相等,如图,若直线l分别交方形环的邻边AD、A'D'、D'C'、DC于点M、M'、N'、N,且M为AD的中点,DN=3CN,则线段MM'与NN'的长度之比为
我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,已知方形环四周的宽度相等,如图,若直线l分别交方形环的邻边AD、A'D'、D'C'、DC于点M、M'、N'、N,且M为AD的中点,DN=3CN,则线段MM'与NN'的长度之比为查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》中考题集(46):20.5 二次函数的一些应用(解析版) 题型:解答题
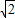 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
查看答案和解析>>
科目:初中数学 来源:2005年湖北省十堰市中考数学试卷(大纲卷)(解析版) 题型:解答题
 x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.
x+1分别交x轴于E,交y轴于F,问△BDC与△EOF是否有可能全等?如果有可能全等请给出证明;如果不可能全等请说明理由.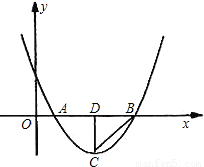
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com