
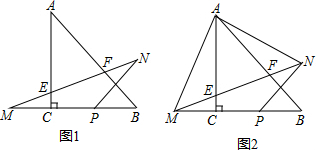
分析 (1)连接NB,如图1,先由△ACB为等腰直角三角形得到∠A=∠CBA=45°,则根据对称的性质得AB垂直PN,BN=BP,则∠NBA=∠PBA=45°,所以∠PBN=90°,接着计算出MC=CP=PB=NB=1,然后利用正切的定义求解;
(2)①连接AP,如图2,利用对称的性质得AP=AM=AN,∠1=∠2,∠3=∠4,则∠MAN=90°,于是可判断△AMN为等腰直角三角形;
②利用△AMN为等腰直角三角形得到∠5=∠6=45°,再证明∠AEF=∠BAM,加上∠B=∠EAF=45°,则根据相似三角形的判定可判断△AEF∽△BAM.
解答 (1)解:连接NB,如图1,
∵在Rt△ABC中,∠ACB=90°,AC=BC,
∴△ACB为等腰直角三角形,
∴∠A=∠CBA=45°,
∵点P关于直线AB的对称点为N,关于直线AC的对称点为M,
∴AB垂直PN,BN=BP,
∴∠NBA=∠PBA=45°,
∴∠PBN=90°,
∵点P为BC的中点,BC=2,
∴MC=CP=PB=NB=1,
∴tan∠M=$\frac{BN}{BM}$=$\frac{1}{3}$;
(2)证明:①连接AP,如图2,
∵点P关于直线AC、AB的对称点分别为M、N,
∴AP=AM=AN,∠1=∠2,∠3=∠4,
∵∠CAB=∠2+∠3=45°,
∴∠MAN=90°
∴△AMN为等腰直角三角形;
②∵△AMN为等腰直角三角形,
∴∠5=∠6=45°,
∴∠AEF=∠5+∠1=45°+∠1,
∵∠EAF=45°
∴∠BAM=∠EAF+∠1=45°+∠1,
∴∠AEF=∠BAM,
又∵∠B=∠EAF=45°
∴△AEF∽△BAM.
点评 本题考查了相似形综合题:熟练掌握对称的性质、等腰直角三角形的判定与性质和相似三角形的判定与性质;记住锐角三角函数的定义.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:填空题
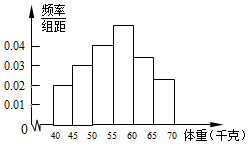 为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为1500人.
为了解全区5000名初中毕业生的体重情况,随机抽测了400名学生的体重,频率分布如图所示(每小组数据可含最小值,不含最大值),其中从左至右前四个小长方形的高依次为0.02、0.03、0.04、0.05,由此可估计全区初中毕业生的体重不小于60千克的学生人数约为1500人.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com