
【题目】已知:四边形 ABCD 内接于⊙O,连接 AC、BD,∠BAD+2∠ACB=180°.
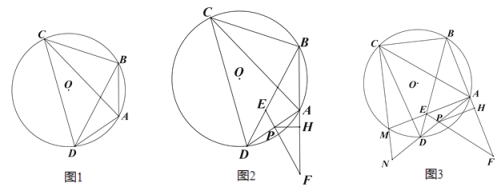
(1)如图 1,求证:点 A 为弧 BD 的中点;
(2)如图 2,点 E 为弦 BD 上一点,延长 BA 至点 F,使得 AF=AB,连接 FE 交 AD 于点 P,过点 P 作 PH⊥AF 于点 H,AF=2AH+AP,求证:AH:AB=PE:BE;
(3)在(2)的条件下,如图 3,连接 AE,并延长 AE 交⊙O 于点 M,连接 CM,并延长 CM 交 AD 的延长线于点 N,连接 FD,∠MND=∠MED,DF=12﹒sin∠ACB,MN=![]() ,求 AH 的长.
,求 AH 的长.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据圆的内接四边形的性质可得∠BAD+∠BCD=180°,然后结合已知条件即可证出∠ACB=∠ACD,从而证出结论;
(2)在HF上取点G,使HG=HA,连接PG、AE,根据垂直平分线的性质可得AP=GP,结合已知条件可得,GP=GF,结合三线合一证出EA⊥BF,再证出EA∥PH,根据平行线分线段成比例定理和等量代换即可得出结论;
(3)连接MB和MD,先利用等角对等边证出MN=MD=![]() ,然后证出△BDF为直角三角形,∠BDF=90°,即可得出BF=12,然后证出△AFM∽△DFB,列出比例式即可求出DF,再根据勾股定理即可求出BD、BM,设AH=x,再利用相似三角形的判定及性质列出比例式即可求出结论.
,然后证出△BDF为直角三角形,∠BDF=90°,即可得出BF=12,然后证出△AFM∽△DFB,列出比例式即可求出DF,再根据勾股定理即可求出BD、BM,设AH=x,再利用相似三角形的判定及性质列出比例式即可求出结论.
解:(1)∵四边形 ABCD 内接于⊙O,
∴∠BAD+∠BCD=180°
∵∠BAD+2∠ACB=180°
∴∠BCD=2∠ACB
∴∠ACB=∠ACD
∴![]()
即点 A 为弧 BD 的中点;
(2)在HF上取点G,使HG=HA,连接PG、AE
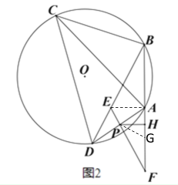
∵PH⊥AF
∴PH垂直平分AG
∴AP=GP
∴∠PAG=∠PGA
∵![]()
∴∠ADB=∠ABD
∴∠PAG=∠ADB+∠ABD=2∠ABD
∵AF=2AH+AP,AF=AH+HG+GF=2AH+GF
∴AP=GF
∴GP=GF
∴∠GPF=∠F
∴∠PGA=∠GPF+∠F=2∠F
∴∠ABD=∠F
∴EB=EF
∵AF=AB,
∴EA⊥BF
∴EA∥PH
∴AH:AF = PE:EF
∴AH:AB=PE:BE;
(3)连接MB和MD

∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴MN=MD=![]()
∵![]() ,AB=AF
,AB=AF
∴AB=AD=AF
∴∠ABD=∠ADB,∠ADF=∠AFD
∴∠ABD+∠AFD=∠ADB+∠ADF=∠BDF
∴△BDF为直角三角形,∠BDF=90°
∵![]()
∴BF=12
∴AB=AD=AF=6
由(2)知:∠EAB=90°
∴∠MDB=90°
∴∠MDB+∠BDF=180°
∴M、D、F三点共线
∵∠AFM=∠DFB,∠FAM=∠FDB=90°
∴△AFM∽△DFB
∴![]()
即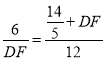
解得:DF=![]() 或-10(不符合实际,舍去)
或-10(不符合实际,舍去)
根据勾股定理可得BD=![]()
BM=![]()
设AH=x,由(2)知:AP=AF-2AH=6-2x
由圆的内角四边形的性质可得:∠PAH=∠BMD
∵∠AHP=∠MDB=90°
∴△AHP∽△MDB
∴![]()
即
解得:x=![]()
即![]()


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:
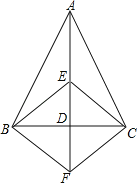
【题目】已知:如图,在△ABC中,AB=AC,AD是BC边上的中线,点E是AD上一点,过点B作BF∥EC,交AD的延长线于点F,连接BE,CF.
(1)求证:△BDF≌△CDE;
(2)当ED与BC满足什么数量关系时,四边形BECF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
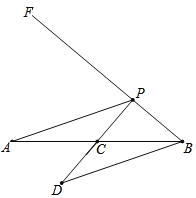
【题目】如图,已知线段AB=6cm,过点B做射线BF且满足∠ABF=40°,点C为线段AB中点,点P为射线BF上的动点,连接PA,过点B作PA的平行线交射线PC于点D,设PB的长度为xcm,PD的长度为y1cm,BD的长度为y2cm.(当点P与点B重合时,y1与y2的值均为6cm)
小腾根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.
下面是小腾的探究过程,请补充完整:
(1)按照下表中自变量x (0≤x≤6)的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 6.0 | 4.7 | 3.9 | 4.1 | 5.1 | 6.6 | 8.4 |
y2/cm | 6.0 | 5.3 | 4.7 | 4.2 | 3.9 | 4.1 |
(说明:补全表格时相关数值保留一位小数)
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出y1,y2的图象;
(3)结合函数图象解决问题:当△PDB为等腰三角形时,则BP的长度约为 cm;
(4)当x>6时,是否存在x的值使得△PDB为等腰三角形 (填“是”或者“否”).
查看答案和解析>>
科目:初中数学 来源: 题型:
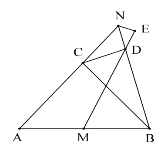
【题目】如图,△ABC 为等腰直角三角形,∠ACB=90°,点 M 为 AB 边的中点,点 N 为射线 AC 上一点,连接 BN,过点 C 作 CD⊥BN 于点 D,连接 MD,作∠BNE=∠BNA,边 EN 交射线 MD 于点 E,若 AB=20![]() ,MD=14
,MD=14![]() ,则 NE 的长为___.
,则 NE 的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形APQD为长方形?
(2)P、Q两点从出发开始到几秒时?四边形PBCQ的面积为33cm2;
(3)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
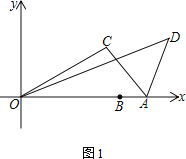
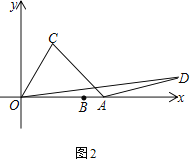
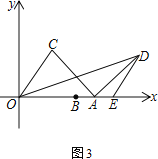
【题目】已知,点A(8,0)、B(6,0).将线段OB绕着原点O逆时针方向旋转角度α到OC,连接AC.将AC绕着点A顺时针方向旋转角度β至AD,连接OD
(1)当α=30°,β=60°时,求OD的长
(2)当α=60°,β=120°时,求OD的长
(3)已知E(10,0),当β=90°时,改变的大小,求ED的最大值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中央电视台《朗读者》节目的播出,“朗读”为越来越多的同学所喜爱,西宁市某中学计划在全校开展“朗读”活动,为了了解同学们对这项活动的参与态度,随机对部分学生进行了一次调查,调查结果整理后,将这部分同学的态度划分为四个类别:![]() .积极参与,
.积极参与,![]() .一定参与,
.一定参与,![]() .可以参与,
.可以参与,![]() .不参与.根据调查结果制作了如下不完整的统计表和统计图.
.不参与.根据调查结果制作了如下不完整的统计表和统计图.
学生参与“朗读”的态度统计表
类别 | 人数 | 所占百分比 |
| 18 |
|
| 20 |
|
|
|
|
| 4 |
|
合计 |
|
|
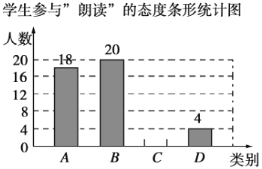
请你根据以上信息,解答下列问题:
(1)![]() ______,
______,![]() ______,并将条形统计图补充完整;
______,并将条形统计图补充完整;
(2)该校有1500名学生,如果“不参与”的人数不超过150人时,“朗读”活动可以顺利开展,通过计算分析这次活动能否顺利开展?
(3)“朗读”活动中,九年级一班比较优秀的四名同学恰好是两男两女,从中随机选取两人在班级进行朗读示范,试用画树状图法或列表法求所选两人都是女生的概率,并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
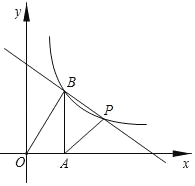
【题目】如图,在平面直角坐标系中,函数y=![]() 的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
的图象经过点P(4,3)和点B(m,n)(其中0<m<4),作BA⊥x轴于点A,连接PA,PB,OB,已知S△AOB=S△PAB.
(1)求k的值和点B的坐标.
(2)求直线BP的解析式.
(3)直接写出在第一象限内,使反比例函数大于一次函数的x的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com