
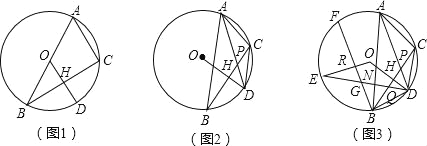
【题目】已知:△ABC内接于⊙O,D是弧BC上一点,OD⊥BC,垂足为H.
(1)如图1,当圆心O在AB边上时,求证:AC=2OH;
(2)如图2,当圆心O在△ABC外部时,连接AD、CD,AD与BC交于点P,求证:∠ACD=∠APB;
(3)在(2)的条件下,如图3,连接BD,E为⊙O上一点,连接DE交BC于点Q、交AB于点N,连接OE,BF为⊙O的弦,BF⊥OE于点R交DE于点G,若∠ACD﹣∠ABD=2∠BDN,AC=![]() ,BN=
,BN=![]() ,tan∠ABC=
,tan∠ABC=![]() ,求BF的长.
,求BF的长.
【答案】(1)证明见解析;(2)证明见解析;(3)24.
【解析】
试题分析:(1)易证OH为△ABC的中位线,可得AC=2OH;(2)∠APB=∠PAC+∠ACP,∠ACD=∠ACB+∠BCD,又∵∠PAC =∠BCD,可证∠ACD=∠APB;(3)连接AO延长交于⊙O于点I,连接IC,AB与OD相交于点M,连接OB,易证∠GBN=∠ABC,所以BG=BQ.在Rt△BNQ中,根据tan∠ABC=![]() ,可求得NQ、BQ的长. 利用圆周角定理可求得IC和AI的长度,设QH=x,利用勾股定理可求出QH和HD的长度,利用垂径定理可求得ED的长度,最后利用tan∠OED=
,可求得NQ、BQ的长. 利用圆周角定理可求得IC和AI的长度,设QH=x,利用勾股定理可求出QH和HD的长度,利用垂径定理可求得ED的长度,最后利用tan∠OED=![]() 即可求得RG的长度,最后由垂径定理可求得BF的长度.
即可求得RG的长度,最后由垂径定理可求得BF的长度.
试题解析:(1)在⊙O中,∵OD⊥BC,∴BH=HC,∵点O是AB的中点,∴AC=2OH;(2)在⊙O中,∵OD⊥BC,∴弧BD=弧CD,∴∠PAC=∠BCD,∵∠APB=∠PAC+∠ACP,∠ACD=∠ACB+∠BCD,∴∠ACD=∠APB;(3)连接AO延长交于⊙O于点I,连接IC,AB与OD相交于点M,连接OB,
∵∠ACD﹣∠ABD=2∠BDN,∴∠ACD﹣∠BDN=∠ABD+∠BDN,∵∠ABD+∠BDN=∠AND,∴∠ACD﹣∠BDN=∠AND,∵∠ACD+∠ABD=180°,∴2∠AND=180°,∴∠AND=90°,∵tan∠ABC=![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴ ,∵∠BNQ=∠QHD=90°,∴∠ABC=∠QDH,∵OE=OD,
,∵∠BNQ=∠QHD=90°,∴∠ABC=∠QDH,∵OE=OD,
∴∠OED=∠QDH,∵∠ERG=90°,∴∠OED=∠GBN,∴∠GBN=∠ABC,∵AB⊥ED,∴BG=BQ=![]() ,GN=NQ=
,GN=NQ=![]() ,
,
∵∠ACI=90°,tan∠AIC=tan∠ABC=![]() ,∴
,∴![]() ,∴IC=
,∴IC=![]() ,∴由勾股定理可求得:AI=25,
,∴由勾股定理可求得:AI=25,
设QH=x,∵tan∠ABC=tan∠ODE=![]() ,∴
,∴![]() ,∴HD=2x,∴OH=OD﹣HD=
,∴HD=2x,∴OH=OD﹣HD=![]() ,BH=BQ+QH=
,BH=BQ+QH=![]() ,
,
∵OB2=BH2+OH2,∴![]() ,解得:
,解得:![]() ,当QH=
,当QH=![]() 时,∴QD=
时,∴QD=![]() ,
,
∴ND=![]() ,∴MN=
,∴MN=![]() ,MD=15,∵
,MD=15,∵![]() ,∴QH=
,∴QH=![]() 不符合题意,舍去,当QH=
不符合题意,舍去,当QH=![]() 时,∴QD=
时,∴QD=![]()
∴ND=NQ+QD=![]() ,ED=
,ED=![]() ,∴GD=GN+ND=
,∴GD=GN+ND=![]() ,∴EG=ED﹣GD=
,∴EG=ED﹣GD=![]() ,∵tan∠OED=
,∵tan∠OED=![]() ,∴
,∴![]() ,
,
∴EG=![]() RG,∴RG=
RG,∴RG=![]() ,∴ BR=RG+BG=12,∴BF=2BR=24.
,∴ BR=RG+BG=12,∴BF=2BR=24.


科目:初中数学 来源: 题型:
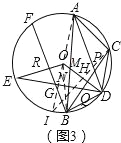
【题目】如图,已知长方形ABCD中AB=8cm,BC=10cm,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,求(1)求BF的长度,(2)求△CEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句:
①“反证法”就是举反例说明一个命题是假命题;②“等腰三角形两底角相等”的逆命题是真命题;③分式有意义的条件是分子为零且分母不为零;④同旁内角互补.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道方程x2+2x﹣3=0的解是x1=1,x2=﹣3,现给出另一个方程(2x+3)2+2(2x+3)﹣3=0,它的解是
A.x1=1,x2=3B.x1=1,x2=﹣3C.x1=﹣1,x2=3D.x1=﹣1,x2=﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题7分)如图,点B、F、C、E在一条直线上,FB=CE,AC=DF,请从下列三个条件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中选择一个合适的条件,使AB∥ED成立,并给出证明.
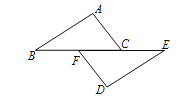
(1)选择的条件是 (填序号)
(2)证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东潍坊第18题)在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com