
 如图,点A、B在反比例函数y=$\frac{k+1}{x}$的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )
如图,点A、B在反比例函数y=$\frac{k+1}{x}$的图象上,且点A,B的横坐标分别为a,2a(a<0),若S△AOB=3,则k的值为( )| A. | 5 | B. | -5 | C. | 4 | D. | -4 |
分析 过A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,延长DB和CA交于点E,由点A、B的横坐标结合反比例函数图象上点的坐标特征即可求出A、B点的坐标,进而得出点E的坐标,再利用分割图形法求△AOB的面积结合S△AOB=3,即可得出关于k的一元一次方程,解方程即可得出结论.
解答 解:过A作AC⊥y轴于点C,过点B作BD⊥x轴于点D,延长DB和CA交于点E,如图所示.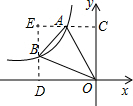
∵点A、B在反比例函数y=$\frac{k+1}{x}$的图象上,且点A,B的横坐标分别为a,2a(a<0),
∴A(a,$\frac{k+1}{a}$),B(2a,$\frac{k+1}{2a}$),E(2a,$\frac{k+1}{a}$),
∴OD=-2a,OC=$\frac{k+1}{a}$,BE=$\frac{k+1}{2a}$,AE=-a,其中k+1<0.
∴S△AOB=S矩形OCED-S△OBD-S△OAC-S△ABE=OD•OC-$\frac{1}{2}$|k+1|-$\frac{1}{2}$|k+1|-$\frac{1}{2}$AE•BE=3,
∵k+1<0,
∴-$\frac{3}{4}$(k+1)=3,
解得:k=-5.
故选B.
点评 本题考查了反比例函数系数k的几何意义以及反比例函数图象上点的坐标特征,解题的关键是利用分割图形求面积法找出关于k的一元一次方程.本题属于基础题,难度不大,解决该题型题目时,将不规则的图形的面积转化成几个规则图形面积之和或之差的形式.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 有理数a、b、c、d所表示的点在数轴上的位置如图所示,若|a-c|=|b-d|=4,|a-d|=5,则b-c的值等于( )
有理数a、b、c、d所表示的点在数轴上的位置如图所示,若|a-c|=|b-d|=4,|a-d|=5,则b-c的值等于( )| A. | -3 | B. | -2 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB为⊙O的直径,C,D为⊙O上的两点,且CD⊥AB于点E,OF⊥AC于点F,连接BD.若∠D=30°,BC=1,则图中阴影部分的面积是( )
如图,AB为⊙O的直径,C,D为⊙O上的两点,且CD⊥AB于点E,OF⊥AC于点F,连接BD.若∠D=30°,BC=1,则图中阴影部分的面积是( )| A. | $\frac{2\sqrt{3}}{3}$π | B. | $\frac{π}{3}$-$\frac{\sqrt{3}}{4}$ | C. | $\frac{2}{3}$π-$\frac{\sqrt{3}}{2}$ | D. | π-$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 姓名 | 平均数(环) | 方差 |
| 甲 | 8 | 0.7 |
| 乙 | 8 | 0.28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com