
分析 (1)首先化简二次根式,进而合并同类二次根式即可;
(2)首先化简二次根式,进而利用二次根式的乘法运算法则求出即可;
(3)首先化简二次根式,进而利用二次根式的乘除运算法则求出即可;
(4)直接利用二次根式的乘法运算法则求出即可.
解答 解:(1)($\sqrt{54}$-$\sqrt{0.5}$+3$\sqrt{\frac{2}{3}}$)-(8$\sqrt{\frac{2}{3}}$-$\sqrt{2}$)
=3$\sqrt{6}$-$\frac{\sqrt{2}}{2}$+3×$\frac{\sqrt{6}}{3}$-8×$\frac{\sqrt{6}}{3}$+4$\sqrt{2}$
=$\frac{4}{3}$$\sqrt{6}$+$\frac{7\sqrt{2}}{3}$;
(2)(3$\sqrt{\frac{3}{5}}$-$\sqrt{15}$)(3$\sqrt{\frac{5}{3}}$+$\sqrt{15}$)
=(3×$\frac{\sqrt{15}}{5}$-3$\sqrt{15}$)($\sqrt{15}$+$\sqrt{15}$)
=-$\frac{12}{5}$$\sqrt{15}$×2$\sqrt{15}$
=-72;
(3)$\frac{\sqrt{3a}}{2b}$($\sqrt{\frac{b}{a}}$÷2$\sqrt{\frac{1}{b}}$)
=$\frac{\sqrt{3a}}{2b}$×$\frac{1}{2}$$\sqrt{\frac{{b}^{2}}{a}}$
=$\frac{\sqrt{3}b}{4b}$
=$\frac{\sqrt{3}}{4}$;
(4)(2$\sqrt{3}$-3$\sqrt{2}$)(3$\sqrt{2}$+2$\sqrt{3}$)
=12-18
=-6.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.


科目:初中数学 来源: 题型:选择题
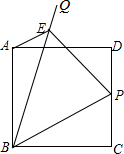 如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )
如图,正方形ABCD边长为2,点P是线段CD边上的动点(与点C,D不重合),∠PBQ=45°,过点A作AE∥BP,交BQ于点E,则下列结论正确的是( )| A. | BP•BE=2$\sqrt{2}$ | B. | BP•BE=4$\sqrt{2}$ | C. | $\frac{BE}{BP}$=$\sqrt{2}$ | D. | $\frac{BE}{BP}$=$\frac{3\sqrt{2}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
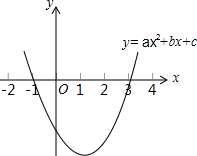 二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列说法:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
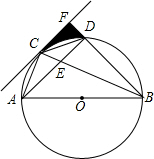 如图,在⊙O中,AB是直径,C是$\widehat{AD}$的中点,弦AD与BC交于点E,过点C的直线CF交BD的延长线于点F,且∠FCD=CBD.
如图,在⊙O中,AB是直径,C是$\widehat{AD}$的中点,弦AD与BC交于点E,过点C的直线CF交BD的延长线于点F,且∠FCD=CBD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
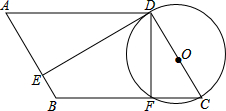 如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边相交于点E,且AE=3EB.
如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边相交于点E,且AE=3EB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com