
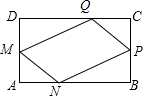
 在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2
在一块矩形ABCD的空地上划一块四边形MNPQ进行绿化.如图,四边形的顶点在矩形的边上,且AN=AM=CP=CQ=xcm,已知矩形的边BC=200m,边AB=am,a为大于200的常数,设四边形MNPQ的面积为sm2分析 (1)根据四边形MNPQ的面积=矩形ABCD的面积-4个三角形面积计算即可.
(2)利用配方法求出二次函数的最值.
解答 解:(1)由题意S=200a-2×$\frac{1}{2}$x2-2×$\frac{1}{2}$(200-a)(a-x)=-2x2+(200+a)x(0<x<a);
(2)∵a=400,
∴S=-2x2+600x=-2(x-150)2+45000.
∴x=150时,S最大值=45000,
∴S最大值为45000cm2,此时x=150cm.
点评 本题考查二次函数的应用,解题的关键是学会利用分割法求三角形面积,学会利用二次函数的性质解决最值问题,属于中考常考题型.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,C、D是线段AB上两点,且AC=BD=$\frac{1}{6}$AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点.在点P从点C移动到点D时,点M运动的路径长度为2.
如图,C、D是线段AB上两点,且AC=BD=$\frac{1}{6}$AB=1,点P是线段CD上一个动点,在AB同侧分别作等边△PAE和等边△PBF,M为线段EF的中点.在点P从点C移动到点D时,点M运动的路径长度为2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com