
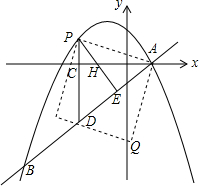
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx+n��k��0����������y=-$\frac{1}{4}{x^2}$+bx+c����A��B���㣬��A��x���ϣ�OA=2����B�ĺ�����Ϊ-8����tan��OAB=$\frac{3}{4}$��
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx+n��k��0����������y=-$\frac{1}{4}{x^2}$+bx+c����A��B���㣬��A��x���ϣ�OA=2����B�ĺ�����Ϊ-8����tan��OAB=$\frac{3}{4}$������ ��1���������A���꣬�ڸ�������ֵ�����B���꣮��һ�����ֱ��AB����ʽ���ɣ���A��B��������뼴������������߽���ʽ��
��2���������P���꣬��ʾ��D���������Ǻ������ɱ�ʾ�����ε��ܳ���
�ڸ�����������֤��ACP�ա�AOQ�����CP���ȣ����������߽���ʽ��⼴�ɣ�
��� �⣺��1����ͼ1
��A��x���ϣ�OA=2��
���A��2��0����
��tan��OAB=$\frac{3}{4}$������ֱ��AB�Ľ���ʽΪ��y=$\frac{3}{4}$x+n��
�����A��2��0����ã�n=$-\frac{3}{2}$��
��ֱ��AB����ʽΪ��y=$\frac{3}{4}$x$-\frac{3}{2}$��
����B��BG��x�ᣬ����ΪG��
��x=-8����ֱ��AB����ã�y=$-\frac{15}{2}$��
���B��-8��$-\frac{15}{2}$����
��������y=-$\frac{1}{4}{x^2}$+bx+c��A��B���㣬
��$\left\{\begin{array}{l}{0=-1+2b+c}\\{-\frac{15}{2}=-16-8b+c}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=-\frac{3}{4}}\\{c=\frac{5}{2}}\end{array}\right.$��
�������߽���ʽΪ��y=$-\frac{1}{4}{x}^{2}-\frac{3}{4}x+\frac{5}{2}$��
��2����ͼ2
����P��t��$-\frac{1}{4}{t}^{2}-\frac{3}{4}t+\frac{5}{2}$������D��t��$\frac{3}{4}t-\frac{3}{2}$����
��PD=$-\frac{1}{4}{t}^{2}-\frac{3}{2}t+4$��
�ߡ�ACP=��PEA=90�㣬��PHC=��AHE��
���OAB=��EPD��
��tan��OAB=tan��EPD=$\frac{3}{4}$��
��$\frac{DE}{PE}=\frac{3}{4}$��
��DE=3a����PE=4a����PD=5a��
��$-\frac{1}{4}{t}^{2}-\frac{3}{2}t+4=5a$��
��a=$-\frac{1}{20}{t}^{2}-\frac{3}{10}t+\frac{4}{5}$��
�֡�m=PD+DE+EP=12a=$-\frac{3}{5}{t}^{2}-\frac{18}{5}t+\frac{48}{5}$��
�ڵ�����Qǡ������y����ʱ��
�ߡ�PAC+��OAQ=��OAQ+��AQO=90��
���PAC=��AQO��
�ڡ�ACP�͡�QOA�У�
$\left\{\begin{array}{l}{��PAC=��AQO}\\{��AOQ=��ACP=90��}\\{AQ=AP}\end{array}\right.$
���ACP�ա�QOA��
��PC=OA=2��
��y=2���������߽���ʽ�ã�$-\frac{1}{4}{x}^{2}-\frac{3}{4}x+\frac{5}{2}$=2��
��ã�x=$\frac{-3+\sqrt{17}}{2}$����x=$\frac{-3-\sqrt{17}}{2}$��
���ʱ��P������Ϊ����$\frac{-3+\sqrt{17}}{2}$��2������$\frac{-3-\sqrt{17}}{2}$��2����
���� ������Ҫ������κ������ۺ����⣬��������꣬���õ��������ߵĽ���ʽ������������ε����ʽ��з����ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪AB�ǡ�O��ֱ������CD��AB��AC=2$\sqrt{2}$��BC=1����ôcos��ABD��ֵ��$\frac{1}{3}$��
��ͼ����֪AB�ǡ�O��ֱ������CD��AB��AC=2$\sqrt{2}$��BC=1����ôcos��ABD��ֵ��$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ڡ�ABC�У�D��F��E�ֱ�Ϊ��BC��AB��AC�ϵ�һ�㣬����BE��FD�������ཻ�ڵ�G������DE�����ı���AFDE��ƽ���ı��Σ�������˵����ȷ���ǣ�������
��ͼ���ڡ�ABC�У�D��F��E�ֱ�Ϊ��BC��AB��AC�ϵ�һ�㣬����BE��FD�������ཻ�ڵ�G������DE�����ı���AFDE��ƽ���ı��Σ�������˵����ȷ���ǣ�������| A�� | $\frac{FG}{GD}=\frac{BF}{AF}$ | B�� | $\frac{AE}{AC}=\frac{BF}{AF}$ | C�� | $\frac{FG}{AE}=\frac{BF}{AF}$ | D�� | $\frac{CE}{EA}=\frac{BF}{AF}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��һ�Ѻ�30��ǵ����dzߣ����AB=8���ڱ�����ߵľ��붼��1����ôEP�ij����ǣ�������
��ͼ��һ�Ѻ�30��ǵ����dzߣ����AB=8���ڱ�����ߵľ��붼��1����ôEP�ij����ǣ�������| A�� | 4 | B�� | 4$\sqrt{3}$ | C�� | $\frac{5}{2}$ | D�� | 6-2$\sqrt{3}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com