
分析 由②可知y≥2,将①代入②解关于y的方程,把y代回②求出x的值可得.
解答 解:解方程组$\left\{\begin{array}{l}{|x-1|+|y-2|=6}&{①}\\{|x-1|=2y-4}&{②}\end{array}\right.$,
由②得:|x-1|=2y-4≥0,
∴y≥2,
将②代入①得:2y-4+y-2=6,解得:y=4,
∴|x-1|=4,
∴x-1=±4,
∴x=5或-3.
故方程组的解为:$\left\{\begin{array}{l}{x=5}\\{y=4}\end{array}\right.$或$\left\{\begin{array}{l}{x=-3}\\{y=4}\end{array}\right.$.
点评 本题主要考查解二元一次方程组的能力,根据y的取值范围去绝对值符号是解题的前提,整体代入的消元方法和思想是解题的关键.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
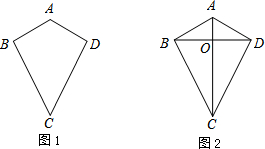
 如图,AB为⊙0的直径,$\widehat{BC}$=$\widehat{CD}$,CE⊥AD于E,OE交AC于点F.
如图,AB为⊙0的直径,$\widehat{BC}$=$\widehat{CD}$,CE⊥AD于E,OE交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
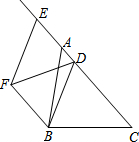 如图,△ABC中,AB=10,sin∠BAC=$\frac{3}{5}$,点D为边AC上一点,点E为CA延长线上一点,且$\frac{AD}{AE}$=$\frac{1}{2}$,以DB、DE为边作?BDEF,则当对角线DF的长取得最小值时,BD的长为8.
如图,△ABC中,AB=10,sin∠BAC=$\frac{3}{5}$,点D为边AC上一点,点E为CA延长线上一点,且$\frac{AD}{AE}$=$\frac{1}{2}$,以DB、DE为边作?BDEF,则当对角线DF的长取得最小值时,BD的长为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com