
【题目】如图,在![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的平分线,
的平分线,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,结论①
,结论①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A.4个B.3个C.2个D.1个
【答案】B
【解析】
①根据三角形的内角和定理判定∠CAM=∠CMA,由等腰三角形的判定和三线合一的性质可得结论正确;
②根据BN=AB=6,CM=AC=5,及线段的和与差可得BC的长;
③根据三角形的内角和定理及角的和与差可得结论;
④要想得到AM=AN,必有∠AMN=∠ANM,而AB≠AC,可知∠ABC≠∠ACB,从而得AM≠AN.
解:①∵CE平分∠ACE,
∴∠ACP=∠MCP,
∵AM⊥CE,
∴∠APC=∠MPC=90°,
∴∠CAM=∠CMA,
∴AC=CM,
∴AP=PM,
①正确;
②同理得:BN=AB=6,
∵CM=AC=5,
∴BC=BN+CM-MN=6+5-2=9,
②正确;
③∵∠BAC=∠MAC+∠BAN-∠MAN=110°,
由①知:∠CMA=∠CAM,∠BNA=∠BAN,
△AMN中,∠CMA+∠BNA=180°-∠MAN=∠BAN+∠MAC,
∴180°-∠MAN-∠MAN=110°,
∴∠MAN=35°,
③正确;
④当∠AMN=∠ANM时,AM=AN,
∵AB=6≠AC=5
∴∠ABC≠∠ACB,
∴∠AMN≠∠ANM,则AM与AN不相等,
④不正确;
所以本题不正确的有④,
故选:B.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数 y=nx+2(n≠0)的图像与反比例函数 y ![]() (m≠0)在第一象限内的图像交于点 A,与 x 轴交于点 B,线段 OA=5,C 为 x 轴正半轴上一点,且 sin AOC
(m≠0)在第一象限内的图像交于点 A,与 x 轴交于点 B,线段 OA=5,C 为 x 轴正半轴上一点,且 sin AOC ![]() .
.
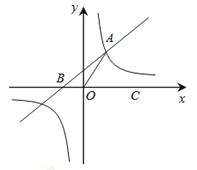
(1)求一次函数和反比例函数的解析式;
(2)求△ AOB 的面积;
(3)请直接写出不等式 nx 2 ![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]()
![]() 求出抛物线
求出抛物线![]() 的对称轴和顶点坐标;
的对称轴和顶点坐标;
![]() 在直角坐标系中,直接画出抛物线
在直角坐标系中,直接画出抛物线![]() (注意:关键点要准确,不必写出画图象的过程);
(注意:关键点要准确,不必写出画图象的过程);
![]() 根据图象回答:
根据图象回答:
①![]() 取什么值时,抛物线在
取什么值时,抛物线在![]() 轴的上方?
轴的上方?
②![]() 取什么值时,
取什么值时,![]() 的值随
的值随![]() 的值的增大而减小?
的值的增大而减小?
![]() 根据图象直接写出不等式
根据图象直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为 1 的正方形组成的网格中,△ ABC的顶点均在格点上,A(3,2), B(4, 3), C(1, 1)

(1)画出△ABC关于y轴对称的图形△ A′B′C′
(2)写出A′、B′、C′的坐标(直接写出答案) A′ ;B′ ;C′ ;
(3)写出△ A′B′C′的面积为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋节前夕,某超市采购了一批土特产,根据以往销售经验,每天的售价与销售量之间有如下表的关系:
每千克售价(元) | 38 | 37 | 36 | 35 | … | 20 |
每天销售量(千克) | 50 | 52 | 54 | 56 | … | 86 |
设当售价从38元/千克下调到x元/千克时,销售量为y千克.
(1)根据上述表格中提供的数据,通过在直角坐标系中描点连线等方法,猜测并求出y与x之间的函数解析式;
(2)如果这种土特产的成本价是20元/千克,为使某一天的利润为780元,那么这一天每千克的售价应为多少元?(利润=销售总金额-成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AB=10,AC=8.线段AD由线段AB绕点A按逆时针方向旋转90°得到,△EFG由△ABC沿CB方向平移得到,且直线EF过点D.
(1)求∠BDF的大小;
(2)求CG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠BAC=130°,AB的垂直平分线ME交BC于点M,交AB于点E,AC的垂直平分线NF交BC于点N,交AC于点F,则∠MAN为( )

A.80°B.70°C.60°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011?菏泽)如图为抛物线y=ax2+bx+c的图象,A、B、C为抛物线与坐标轴的交点,且OA=OC=1,则下列关系中正确的是( )
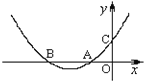
A. a+b=﹣1 B. a﹣b=﹣1
C. b<2a D. ac<0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com