
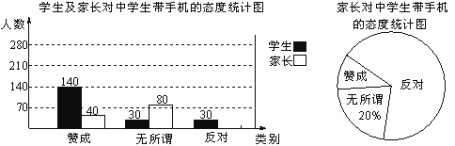
【题目】“校园手机”现象越来越受到社会的关注,小记者张明随机调查了某校若干学生和家长对中学生带手机现象的看法,制作了如图所示的统计图:
(1)这次调查的总人数有_____人;
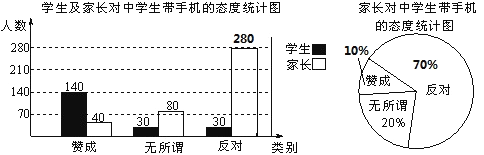
(2)补全两个统计图;
(3)针对随机调查的情况,张明决定从初三一班表示赞成的4位家长中随机选择2位进行深入调查,其中包含小亮和小明的家长,小亮和小明的家长被同时选中的概率是_____.(以上三个问题均不需写过程)
【答案】(1)600;(2)补图见解析;(3)![]()
【解析】
(1)先根据条形统计图求出调查的学生人数,再根据家长中无所谓的人数与占比求出调查的家长人数,再把他们相加即可;(2)根据求得的调查的家长人数减去赞成与无所谓的人数,即可求出反对的人数,即可补全条形统计图与扇形统计图;(3)根据题意可画出树状图,再根据概率公式进行求解即可.
(1)调查的学生人数为:140+30+30=200(人)
调查的家长人数为:80÷20%=400(人)
故调查总人数为:200+400=600(人)
(2)家长赞成带手机的占比为:40÷400=10%
反对带手机的人数为400-40-80=280(人)
反对带手机的占比为:(400-40-80)÷400=70%
故补全统计图如下:
(3)根据题意画出树状图如下:
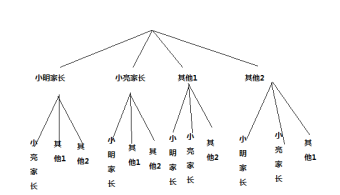
故P(小亮和小明的家长被同时选中)=![]()


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止)。则四边形PABQ的面积y(
,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止)。则四边形PABQ的面积y(![]() )与运动时间x(s)之间的函数图象为( )
)与运动时间x(s)之间的函数图象为( )
A. 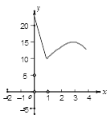 B.
B. 
C. 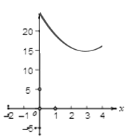 D.
D. 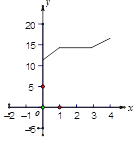
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在三角形ABC中,AB=6,AC=BC=5,以BC为直径作⊙O交AB于点D,交AC于点G,直线DF是⊙O的切线,D为切点,交CB的延长线于点E.
(1)求证:DF⊥AC;
(2)求tan∠E的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字![]() ,2,4的不透明卡片,它们除数字外都相同;现将它们背面朝上,洗匀后,从三张卡片中随机地抽出一张,记住数字;
,2,4的不透明卡片,它们除数字外都相同;现将它们背面朝上,洗匀后,从三张卡片中随机地抽出一张,记住数字;
![]() 若把抽出的卡片放回,洗匀后,再从三张卡片中随机抽出一张,记住数字
若把抽出的卡片放回,洗匀后,再从三张卡片中随机抽出一张,记住数字![]() 试用列表或树状图的方法,求两次抽取的卡片上的数字为一正数、一负数的概率.
试用列表或树状图的方法,求两次抽取的卡片上的数字为一正数、一负数的概率.
![]() 若不把抽出的卡片放回,再从剩余两张卡片中随机抽出一张,直接写出两次抽取卡片上的数字为一正数、一负数的概率.
若不把抽出的卡片放回,再从剩余两张卡片中随机抽出一张,直接写出两次抽取卡片上的数字为一正数、一负数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象分别交x轴、y轴于A、B两点,且与反比例函数
的图象分别交x轴、y轴于A、B两点,且与反比例函数![]() 的图象在第一象限交于点C(4,n),CD⊥x轴于D.
的图象在第一象限交于点C(4,n),CD⊥x轴于D.
(1)求m、n的值,并在给定的直角坐标系中作出一次函数的图象;

(2)如果点P、Q分别从A、C两点同时出发,以相同的速度沿线段AD、CA向D、A运动,设AP=k.
①k为何值时,以A、P、Q为顶点的三角形与△AOB相似?
②k为何值时,△APQ的面积取得最大值并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
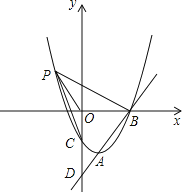
(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年12月16日,南京大报恩寺遗址公园正式对外开放.某校数学兴趣小组想测量大报恩塔的高度.如图,成员小明利用测角仪在B处测得塔顶的仰角α=63.5°,然后沿着正对该塔的方向前进了13.1m到达E处,再次测得塔顶的仰角β=71.6°.测角仪BD的高度为1.4m,那么该塔AC的高度是多少?(参考数据:sin63.5°≈0.90,cos63.5°≈0.45,tan63.5°≈2.00,sin71.6°≈0.95,cos71.6°≈0.30,tan71.6°≈3.00)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录了一名球员在罚球线上投篮的结果,这么球员投篮一次,投中的概率约是( )
投篮次数 | 10 | 50 | 100 | 150 | 200 | 250 | 300 | 500 |
投中次数 | 4 | 35 | 60 | 78 | 104 | 123 | 152 | 251 |
投中频率 | 0.40 | 0.70 | 0.60 | 0.52 | 0.52 | 0.49 | 0.51 | 0.50 |
A. 0.7B. 0.6C. 0.5D. 0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实施产业精准扶贫,帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克,到了收获季节投入市场销售时,调查市场行情后,发现该蜜柚不会亏本,且每天的销售量y(千克)与销售单价x(元)之间的函数关系如图所示.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?
(3)某村农户今年共采摘蜜柚12000千克,若该品种蜜柚的保质期为50天,按照(2)的销售方式,能否在保质期内全部销售完这批蜜柚?若能,请说明理由;若不能,应定销售价为多少元时,既能销售完又能获得最大利润?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com