Question

4．平行四边形ABCD是正方形需增加的条件是（　　）

• A． 邻边相等
• B． 邻角相等
• C． 对角线互相垂直
• D． 对角线互相垂直且相等

Answer 1

分析 可以针对正方形的判定方法，由给出条件四边形ABCD为平行四边形，加上条件AC=BD根据对角线相等的平行四边形为矩形，得到ABCD为矩形，再加上对角线AC与BD垂直，根据对角线垂直的矩形是正方形即可得证．

解答 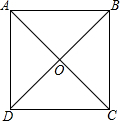解：如图所示：
添加的条件是AC=BD且AC⊥BD，平行四边形ABCD为正方形；
理由如下：
添加的条件时AC=BD且AC⊥BD时；
∵四边形ABCD是平行四边形．又AC=BD，
∴四边形ABCD是矩形，
∵AC⊥BD，
∴四边形ABCD是菱形，
∴四边形ABCD是正方形；
故选：D．

点评 此题主要考查矩形及正方形的判定；熟练掌握矩形、正方形的判定方法，并能进行推理论证是解决问题的关键．